Forme factorisee fonction

[franceguy]

Bonsoir

j'ai une fonction à mettre sous forme factorisée et je bloque.
Voici l'énoncé:

soit f(x)=3x²+2x-1
prouver que f(x)=(3x-1) (x+1)

J'ai essayé de faire: f(x)=3x²+3x-x-1
=3x(x+1)-x-1

Mais je suis bloquée .POUVEZ-VOUS M'AIDER SVP? MERCI

[lop]

Bonjour, tu es en seconde je presume ?
normalement ce que tu dois faire c'est
développer ça :(3x-1) (x+1)
tu vas trouver: 3x²+2x-1
et donc tu dis f(x)=(3x-1) (x+1)

:)

[franceguy]

Bonjour, tu es en seconde je presume ?
normalement ce que tu dois faire c'est
développer ça 3x-1) (x+1)
tu vas trouver: 3x²+2x-1
et donc tu dis f(x)=(3x-1) (x+1)

Est-il possible de partir de f(x)=3x²+2x-1 et d'arriver à f(x) =(3x-1)(x+1) comme c'est demandé dans l'exercice?

[lop]

tu es en seconde ?
si tu es en seconde c'est ce qu'ils attendent

[Pisigma]

Bonsoir

j'ai une fonction à mettre sous forme factorisée et je bloque.
Voici l'énoncé:

soit f(x)=3x²+2x-1
prouver que f(x)=(3x-1) (x+1)

J'ai essayé de faire: f(x)=3x²+3x-x-1
=3x(x+1)-x-1=3x(x+1)-(x+1)=(3x-1)(x+1)

Mais je suis bloquée .POUVEZ-VOUS M'AIDER SVP? MERCI

Bonsoir,

Tu y étais presque.Voir ma réponse en rouge

[lop]

Salut Pisigma,
en seconde quand j'avais des questions comme ça on ma toujours dit qu'on pouvait partir de la forme factorisée et la développer... tu penses que c'est faux ?

[laetidom]

Est-il possible de partir de f(x)=3x²+2x-1 et d'arriver à f(x) =(3x-1)(x+1) comme c'est demandé dans l'exercice?

Bonjour,

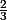
Niveau seconde (passage par la forme canonique de x² + x - ) :

Soit 3x²+2x-1

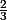
= 3(x²+x - )

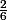
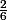
= 3[(x+)² - ()² - ]

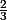
= 3[(x+)² - ()²] = 3[ " a² - b² " ] = ...

= 3(x-)(x+1)

= (3x-1)(x+1)

[franceguy]

Bonjour,

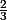
Niveau seconde (passage par la forme canonique de x² + x - ) :

Soit 3x²+2x-1

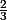
= 3(x²+x - )

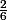
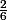
= 3[(x+)² - ()² - ]

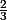
= 3[(x+)² - ()²] = 3[ " a² - b² " ] = ...

= 3(x-)(x+1)

= (3x-1)(x+1)

MERCI BEAUCOUP!

[laetidom]

MERCI BEAUCOUP!

Content d'avoir pu être utile ! @+ sur le forum.