Forme exponentielle d'un nombre complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sawamura07
- Membre Naturel
- Messages: 19
- Enregistré le: 05 Mar 2015, 20:49
-
 par Sawamura07 » 22 Oct 2015, 20:56
par Sawamura07 » 22 Oct 2015, 20:56
Bonsoir
je bloque un peu avec les formes exponentielles d'un nombre complexe
le probleme c'est l'exercice 7

voilà mon essaie pour la 1ere question mais je suis pas très sûr

pour la 2 je sais que i = e(i*pi) mais je sais pas comment faire après
merci d'avance pour votre aide

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 22 Oct 2015, 21:09
par Sake » 22 Oct 2015, 21:09
Sawamura07 a écrit:Bonsoir
je bloque un peu avec les formes exponentielles d'un nombre complexe
le probleme c'est l'exercice 7

voilà mon essaie pour la 1ere question mais je suis pas très sûr

pour la 2 je sais que i = e(i*pi) mais je sais pas comment faire après
merci d'avance pour votre aide
Salut,
Tout nombre complexe z se met sous la forme
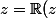 + i\I (z) = |z|(\cos \theta + i\sin \theta) = |z|e^{i\theta})
En considération de ce que tu vois, il faut identifier

comme un
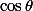
et

comme un
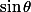
Il suffit en fait de remarquer que 1 - cos y = 2*(1 - cos(2*y/2))/2 = 2*sin²(y/2) et que sin y = sin(2*y/2) = 2 sin(y/2)cos(y/2)
En conclusion, z = 1/2(sin y + i(1 - cos y)) = sin (y/2)*(cos(y/2) + i*sin(y/2))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 115 invités


