Forme canonique, Seconde

[Celizera]

Bonjour à tous, j'ai une expression à factoriser et je n'y arrive tout simplement pas.. Je suppose que je dois utiliser la forme canonique mais pareil, je ne trouve pas:
f(x)=0,5x²-4x+6

Merci à tous :we:

[Xulthiar]

L'équation est-elle ou ?

[Celizera]

Ah je suis désolée je me suis trompée.
En faite c'est un fonction, que je voudrais factoriser, ça donne

f(x)=1/2x^2-4x+6

Sans parenthèses

[Celizera]

Ce n'est pas vraiment une équation, mais l'expression d'une fonction, dont je dois trouver le signe, et je suis obligée de factoriser.

[Xulthiar]

Ce n'est pas vraiment une équation, mais l'expression d'une fonction, dont je dois trouver le signe, et je suis obligée de factoriser.

Ah tu as modifié. Ok. . Ma question reste cependant valable : le est-il dans la parenthèse du carré ou non ?

[Celizera]

Ah je comprends, non justement, c'est bien 1/2x² et non (1/2x)²

[Xulthiar]

Il y a une différence entre la forme factorisée (de la forme et la forme canonique (de la forme
Pour factoriser, tu dois chercher les racines (les x pour lesquels le polynôme s'annule) du polynôme. Quels outils as-tu à ta disposition pour le faire ?

[Celizera]

Ce que je sais c'est que la forme canonique on l'a vu assez vite, et mon but serait d'arriver à ce qui pourrait donner un identité remarquable Voila pourquoi je me suis dit que peut-être je devais passer par là. En tout cas, je dois factoriser. Et après les outils.. étant en seconde je pense que je suis limitée, les racines du polynôme ça ne me parle pas trop..

[Xulthiar]

Ce que je sais c'est que la forme canonique on l'a vu assez vite, et mon but serait d'arriver à ce qui pourrait donner un identité remarquable Voila pourquoi je me suis dit que peut-être je devais passer par là. En tout cas, je dois factoriser. Et après les outils.. étant en seconde je pense que je suis limitée, les racines du polynôme ça ne me parle pas trop..

As-tu étudié le discriminant ?

[Celizera]

Ah non pas encore de delta pour moi.. Mais là c'est possible d'utiliser la forme canonique ou pas?

[Xulthiar]

Dans ce cas, tu as deux méthodes : ou bien trouver directement les x pour lesquels ce polynôme s'annule (l'une est facile, l'autre se déduit de la première), ou bien utiliser les techniques que tu maîtrises. Donc, dans ce cas, la forme canonique (maitrises-tu d'autres outils ?).

Que sais-tu de la forme canonique ? Tu connais sa formule ? (comment passer de l'une forme à l'autre, sans réfléchir)
On peut aussi "bricoler", et passer par les identités remarquables.

[Celizera]

Je crois que je ne sais même pas trouver les x pour lequel le polynôme s'annule.. puisque qu'il faut faire une équation produit nulle j'imagine. Et donc factoriser.. Enfin là je suis un peu embrouillée. La forme canonique, ce n'est pas au programme donc on ne l'a pas vu "officiellement" Je sais à priori passer d'une forme dévellopé à cette forme canonique mais là je n'arrive pas. Mais pour ça j'ai besoin de pas mal de calculs, je ne connais pas sa formule, je bricole justement.

[Xulthiar]

Justement, pour la forme factorisée, on peu penser l'inverse. En se creusant la cervelle, on trouve une valeur de x pour laquelle le polynôme s'annule, et on en déduit la forme factorisée.

On va bricoler alors :
f(x)=0,5x²-4x+6


Connais-tu les identités remarquables ? Comme par exemple, ? Si oui, essayes de t'y ramener pour obtenir une forme canonique.

[Celizera]

Oui bien sûr les identités remarquables je connais. Alors j'ai obtenu une forme canonique et je me suis retrouvé avec , Et la? Est-ce que par hasard ça nous donne le droit d'arriver à une équation produit nul?

[Xulthiar]

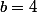
Tu ne dois pas trouver , tu as du faire une erreur quelque part. Ah, je pense savoir, n'as tu pas appliqué la formule pour et non ?
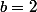
Je ne comprends pas ta distinction entre équation produit nul et équation factorisée.

[Celizera]

Ah oui, c'est enfaite je viens de me rendre compte que je dois trouver f(x)<0, ce qui ne change pas grand chose. Ensuite ça me donne et je n'ai plus qu'à trouver les solutions?

[Xulthiar]

Exactement. (Je te conseille de garder le 2, vu que c'est une fonction).
Tu fais un tableau de signe (tu as vu ça ?) et tu conclus.

[Celizera]

Oui j'ai vu! Ça change vraiment quelque chose de garder le 2? En tout cas, MERCI, je n'en pouvais plus!

[Xulthiar]

A partir du moment où c'est une fonction, tu n'as pas le choix.

Si tu établis l'équation , alors tu peux enlever le 2, sinon non.

[Celizera]

D'accord, j'ai tout compris, merci beaucoup!