Fontions 1èreS

[Solène]

Bonjour, je bloqque sur une question d'un D.M. Si quelqu'un peut m'aider ??

Soit f(x)=(2x+(pi/3)

Montrer que le point P (pi/3 ;0 ) est un centre de symétrie de la courbe C.

( C est la courbe représentative de la fonction f )

Merci d'avance!!

[Gnörf]

Il existe une méthode pour trouver le centre de symétrie d'une courbe: Tu fais un changement de repère au point que tu supposes centre de symétrie (ici tu prend P). Tu peux ainsi en déduire la nouvelle équation de ta fonction ... il ne te reste plus qu'a verifier que ta "nouvelle" équation te donne une courbe qui est bien symétrique par rapport a l'origine (tient tient ça me rappelle une histoire de parité tout ça). Il se peut que je n'ai pas était clair ... En espérant que tu ai vu les changements de repères.
Gnörf

Remaque: Ne t'es tu pas tromper en recopiant l'énoncé? Le point P(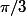,0) m'a lair louche ... le centre serait plutot le point P(0,)

[Solène]

Non je ne me suis pas trompé en recopiant. J'ai bien compris ton explication. Merci pour ton aide.
:fan:

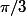[Gnörf]

attention ... je trouve le point P(0,/3) ... normalement le point (/3,0) ne te donne pas une fonction impaire dans le nouveau repère ...

[Solène]

Oui j'ai le meme problème car la courbe n'est pas centré sur zéro... La prof a du se tromper....