Fonctions trigo inverses

par **nada-top** » 21 Aoû 2006, 23:17

[FONT=Comic Sans MS][B]bonsoir,[/B]

quelles sont les méthodes possibles pour simplifier les fonctions trigonométriques inverses [/FONT] :

etc [FONT=Comic Sans MS](avec u donnée bien sur )...en fait il y a cette méthode de changement de variabe par ex poser [/FONT] :

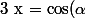..[FONT=Comic Sans MS]mais là parfois il faut étudier plusieurs cas selon les intervalles et franchement ça m'ennuie[/FONT] :dodo: [FONT=Comic Sans MS]y-a-t-il pas plus pratique [/FONT] ?

[FONT=Comic Sans MS][B]xie xie [/B] [/FONT] :lol3:

par **nada-top** » 21 Aoû 2006, 23:24

ah avant d'oublier :id: j'ai vu qq part une méthode (je me souviens ni ou ni comment) avec les dérivées et un K ... vraiment je me souviens plus , je voudrais plus de précisions la dessus .

xie xie :jap:

par **Nightmare** » 22 Aoû 2006, 08:56

Bonjour

La dérivation peut parfois être utile.

:happy3:

par **nada-top** » 22 Aoû 2006, 09:37

bonjour,

la dérivation c-a-d ? .. si je me trompe pas tu entends par ça appliquer la propriété si deux fonctions sont dérivables sur un intervalle I et qui ont la meme dérivée alors

etc . désolée si j'ai oublié un détail mais vraiment je me rappelle pas de ça je l'ai croisé qq parts et je crois pas que c'est au programme... et en plus parfois il est un peu difficille de déterminer l'autre fonction ayant la meme dérivée ....

sinon peux-tu expliquer ce que tu voulais dire par dérivation ?

par **ayanis** » 22 Aoû 2006, 09:41

Bonjour,

Pour avoir une réponse plus précise tente peut etre de poster dans supérieur, parce que ces fonctions ne sont étudiées qu'en post-bac... Mais dans mon souvenir on fait presque que de la dérivation, sinon, on ne s'en sert que comme résultat d'une équation... Comme on ne cherche presque jamais à simplifier ces expressions puisqu'on considère qu'on les "connait" il n'y a pas d'autres méthodes à mon souvenir, mais là encore je peux me tromper....

ttyl

par **nada-top** » 22 Aoû 2006, 10:00

bonjour, :happy3:

peux-tu expliquer ce que vous voulez dire par dérivation , c'est cette propriété de la constante

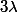
ou c'est autre chose? ...

pour ce qui est du niveau , je crois que cette question est trés bien placée dans la rubrique lycée puisque c'est la première leçon qu'on voit au TS.

par **ayanis** » 22 Aoû 2006, 10:09

Re,
Ah, pardon, les programmes ont du changer... :)
Je ne vois pas ce que tu appelles propriété de la constante lambda mais, les fonctions x->Arccos(x) et x->Arcsin(x) sont continues sur un intervalles, et elles sont même dérivables. Les dérivées sont des racines carrées beaucoup plus faciles à traiter que les fonctions trigonométriques inverses

(Arccos(x))'=-1/(racine de (1-x²))
on a aussi des formules comme :
sin(Arccos x)= racine(1-x²) ou tan(Arccos x)= (racine (1-x²))/x

Désolée, je ne maitrise pas encore bien le latex...

ttyl

par **nada-top** » 22 Aoû 2006, 10:21

ce que j'appelle propriété de la constante

, c'est ce j'ai cité dans mon 2eme post :lol3: ...j'ai cru que t'as lu

par **ayanis** » 22 Aoû 2006, 10:32

Désolée je pensais l'avoir lue mais en fait je m'étais limitée à la question tout au début...

Euh, la méthode de la constante n'est pas très pratique parce qu'il est rare que g soit simple à trouver comme tu l'as déjà fait remarquer. La dérivation sert dans ce genre d'exos :

Montrer que pour tout x de [0,1]
Arctan(racine (x))=Pi/4+1/2 Arcsin(2x-1)
Exos classique dans ce genre de chapitre... :)

Ou encore étudier la fonction... (suivi d'un truc barbare)
Si tu veux des exos pour t'entrainer, fais moi signe, j'ai un bon bouquin la dessus

ttyl

par **nada-top** » 22 Aoû 2006, 10:48

oui c'est ce que je disais c'est un peu compliqué avec cette méthode ....

ah vraiment si tu as d'autres exemples je suis preneur :we: ...car franchement j'ai seulement 4 exs qui sont un peu compliqués et je voudrais les travailler c'est pour cela que je n'ai posté aucun comme ex.... mais d'abord j'ai réfléchi à bien maitriser qq méthodes pratiques pour m'en sortir car vraiment soit avec le changement de varialbe soit avec la dérivation c'est un compliqué...
voilà un ex :

par **ayanis** » 22 Aoû 2006, 10:54

Je suppose que l'énoncé est d'étudier la fonction... D'abord, commence par le domaine de définition! toujours avec ce genre de fonctions... Ensuite, c'est une composée, tu dérives, tu n'auras plus de Arcsin après dérivation, tu peux donc étudier la croissance. Ensuite c'est une étude basique, tu calcules la valeur en x=0 ou autre si c'est un autre qui est plus simple... et puis tu traces. Je ne t'en dis pas plus (je ne t'ai même rien dit en fait si on regarde bien) pour que tu puisses t'amuser :) :we:

ttyl

par **nada-top** » 22 Aoû 2006, 11:04

non au fait ce qui m'a soulagé le plus :ptdr: c'est que l'énoncé était plus simple que ça :

simplifier :

:ptdr:

par **ayanis** » 22 Aoû 2006, 11:08

Ok, mais sinon n'hésites pas, c'est pas très difficile de tenter ce que j'ai dit...
Surtout après simplification... (et dire que j'avais même pas vu qu'on pouvait simplifier...)

par **nada-top** » 22 Aoû 2006, 11:42

oui merci je vais tenter ça ... mais franchement je vois pas de logique dans ce programme car en fouillant dans le livre de TS cette question est posée avant la leçon de l'étude de ce genre de fonctions et meme bien avant la dérivation :doh: .... c'est juste une introduction des fonctions inverses en général ce qui me parait bizzare .

@+

par **ayanis** » 22 Aoû 2006, 11:45

Non, c'est normal la simplification ne demande aucune connaissance sur ces fonctions. Donc je pense que c'est mis juste pour familiariser les élèves avec la notation de ces fonctions et pour qu'ils n'en ai pas peur...

ttyl

par **nada-top** » 22 Aoû 2006, 14:09

Hola

je suis arrivée à une etape de calculs et il me faut ça :

?? qqn a une idée ??

xie xie :lol3:

par **Nightmare** » 22 Aoû 2006, 14:13

Bonjour

je ne suis pas sûr que ce soit vraiment simplifiable, comment as-tu obtenu cela ?

par **nada-top** » 22 Aoû 2006, 14:31

non je cherche pas celle , j'ai commencé par une autre plus facile :

donc j'ai posé

avec

donc

...etc donc il me faut

pour continuer .

par **ayanis** » 22 Aoû 2006, 14:37

Voups, désolée, j'avais pas fait les calculs... te prends pas la tête, je crois pas que ca se simplifie...

Par contre, tu peux essayer de démontrer que Arctan x+Arctan (1/x)=Pi/2 pour tout x>0

et aussi que Pour tout x de [-1,1] Arccos x + Arcsin x = Pi/2

Voili, voilou, encore désolée pour l'étude de l'autre... si tu veux je t'en donnerai une autre où je suis sure que c'est faisable...

ttyl

par **nada-top** » 22 Aoû 2006, 17:08

pour la 1ère :

je vais partir par éqivalence :
on a

(puisque

donc

)

ce qui est vrai

pour la 2ème je suppose qu'il y a qq chose qui cloche concernant l'intervalle de x car

on a

:hein:

Fonctions trigo inverses

fonctions trigo inverses

Qui est en ligne