Fonctions trigo inverses
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 22 Aoû 2006, 22:49
par nada-top » 22 Aoû 2006, 22:49
bonsoir à vous tous
---- Nightmare : au cas ou tu es sur de ce

(car c'est ce calcul qui m'a effrayé et j'ai laissé tomber ) je crois que c'est bon mais il faut quand meme préciser le domaine de dérivabilité de f juste pour etre rigoureux . :lol3:
mais franchement si ce calcul est juste j'aurais pas eu la patience d'y arriver vue j'admire plus les calculettes . :++:
à propos de

et

, effectivement il y a une différence et ce qu'a dit Nightmare m'affirme ce que j'ai trouvé

et il y a aussi cette différence au niveau de Arg et arg...
merci à vous tous
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 22 Aoû 2006, 22:52
par Nightmare » 22 Aoû 2006, 22:52
Oui Ayanis, autant pour moi, merci d'avoir corrigé.
Nada-top, je suis sûr de mon égalité (ma calculette soutenant mes calculs au brouillon)
:happy3:
-
ayanis
- Membre Relatif
- Messages: 234
- Enregistré le: 19 Aoû 2006, 21:22
-
 par ayanis » 22 Aoû 2006, 22:59
par ayanis » 22 Aoû 2006, 22:59
Pardon, j'ai oublié de te féliciter pour cette égalité! et merci pour ce calcul! tu as eu une idée de génie :id:
ttyl
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 22 Aoû 2006, 23:04
par Nightmare » 22 Aoû 2006, 23:04
C'est ce que j'entendais dès le début de la conversation par "La dérivation peut parfois être utile."
Merci en tout cas.
:happy3:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 22 Aoû 2006, 23:11
par nada-top » 22 Aoû 2006, 23:11
Nada-top, je suis sûr de mon égalité (ma calculette soutenant mes calculs au brouillon)
dans ce cas bien joué :++: ... franchement je vais pas vérifier à la main ça me donne pas envie , je te fais confiance.
en tous cas il y a surement une autre méthode puisque cette methode ne figure pas au programme à ce qu'il me parait et en plus la question est posée avant meme la dérivation .
sinon tu n'as pas la formule de
)
merci à vous tous. :happy3:
-
ayanis
- Membre Relatif
- Messages: 234
- Enregistré le: 19 Aoû 2006, 21:22
-
 par ayanis » 22 Aoû 2006, 23:13
par ayanis » 22 Aoû 2006, 23:13
de rien :++:
ttyl
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 22 Aoû 2006, 23:25
par Nightmare » 22 Aoû 2006, 23:25
Je viens de trouver une autre méthode :
On sait que :
=\frac{1-tan^{2}\(\frac{x}{2}\)}{1+tan^{2}\(\frac{x}{2}\)})
On veut simplifier :
=Arccos(\frac{1-x}{1+x}))
En posant
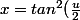)
:
=Arccos(cos(u))=u)
Or :
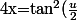\Rightarrow tan(\frac{u}{2})=\sqrt{x}\Rightarrow \frac{u}{2}=Arctan(\sqrt{x})\Rightarrow u=2Arctan(\sqrt{x}))
On retrouve notre résultat à pi/2 près, qui a dû se perdre quelque part dans la démonstration.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 23 Aoû 2006, 00:05
par nada-top » 23 Aoû 2006, 00:05
il me parait
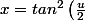\Rightarrow\; \sqrt{x} = |tan \left(\frac{u}{2}\right ) |)
...puisqu'on sait pas encore u sinon j'ai raté qq chose et je dois vraiment aller me coucher :dodo:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 23 Aoû 2006, 12:23
par nada-top » 23 Aoû 2006, 12:23
vraiment j'sais pas pourquoi tu néglige beaucoup les conditions et les intervalles ou tu travaille pourtant c'est déterminant :hein:
d'abord je vois pas comment tu passe
 \rightarrow tan\left(\frac{u}{2}\right) = \sqrt{x})
:hein: je penses que cela implique
| = \sqrt{x})
puisque


et en plus tu n'as le droit de dire
) =u)
que si tu travaille sur l'intervalle ou

..et pour

il était mieux de dire
) =-u)
sinon il est fort bien que je me trompe peux tu t'expliquer?
-
ayanis
- Membre Relatif
- Messages: 234
- Enregistré le: 19 Aoû 2006, 21:22
-
 par ayanis » 23 Aoû 2006, 12:50
par ayanis » 23 Aoû 2006, 12:50
Nada-top a raison, c'est parce que tu as oublié de tenir compte des intervalles où tu travailles que le Pi/2 a disparu, mais le reste est correct... Tu as les idées mais pas encore la rigueur :we: c'est normal en 1ère, mais si tu veux faire une prépas ou plus généralement des maths en post bac il faudra que tu t'y mettes...
Bien joué en tout cas pour cette solution, :++: ce changement de variable est souvent utile en trigo
ttyl
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Aoû 2006, 00:01
par Nightmare » 24 Aoû 2006, 00:01
Je voudrais préciser que ce n'est pas à moi de tout faire non plus, je donne les idées principales, effectivement un pi/2 s'est perdu et je n'ai pas cherché à savoir où, c'était à Nada-top de le trouver.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 24 Aoû 2006, 12:09
par nada-top » 24 Aoû 2006, 12:09
bonjour ,
Nightmare a écrit:Je voudrais préciser que ce n'est pas à moi de tout faire non plus
personne ne t'a demandé ça et d'ailleurs c'est un exo de recherche et je suis pas obligée d'avoir la réponse par n'importe quel moyen et je suis loin de me contenter des démos des autres ce qui m'importe le plus c'est 'tenter' peu importe ce qu'on attendait . :lol4:
--------------------------------------------------
donc voilà ce qui cloche :
tu as posé
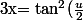)
;

[FONT=Comic Sans MS]
1er cas [/FONT] :

 = Arccos(cos(u)) = u)
 \Leftrightarrow\; \sqrt{x} = tan(\frac{u}{2}) \; \Leftrightarrow \; 2 Arctan(\sqrt{x}= u)
( il y a ici une équivalence pas seulement une implication puisque

est bijective de
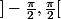
sur R )
donc dans ce cas
 = 2 Arccos (\sqrt{x}))
[FONT=Comic Sans MS]
2eme cas [/FONT] :

 = Arccos(cos(-u)) = -u)
 \Leftrightarrow\; \sqrt{x} = - tan(\frac{u}{2}) \; \Leftrightarrow \; \sqrt{x} = tan(\frac{-u}{2}) \; \Leftrightarrow 2 Arctan(\sqrt{x})= - u)
donc
 = 2 Arctan(\sqrt{x})
finalement on peut en déduire que
 = 2 Arctan(\sqrt{x})})
on se demande ou est le

!! ...tout simplement il n'existe pas

puisque t'as fait une faute dans ta 1ère méthode .
 - 2 Arctan (0) = 0)
donc
 = 2 Arctan (\sqrt{x}) })
(sauf erreur)
@+ :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 249 invités
