Fonctions [1ere S]
35 messages
- Page 1 sur 2 - 1, 2
Fonctions [1ere S]
Bonjour, j'ai un petit exercice à faire et je ne m'en sors pas, c'est pourquoi je requiers votre aide.
Voici l'exercice :
Les deux fonctions f et g sont définies par : f(x)= (-2x -1)² - (-x+3)²
g(x)= x²-16-(2x+8)(-2x+1).
1. Développer, réduire et ordonner f(x)
2. Factoriser f(x) et g(x)
3.a. Quels sont les antécédents de -8 par f ?
3.b. Pour quelles valeurs de x l'expression f(x) est-elle négative ou nulle?
3.c. Déterminer l'intervalle sur lequel la courbe de la fonction g est située strictement en dessous de l'axe des abscisses.
4. Soit a= racine de 2 / racine de 2+1 (je ne sais pas comment on fait les racines désolé)
Ecrire a avec un dénominateur entier.
Calculer f(a) et en donner une valeur arrondie à 10-1 (-1 est en exposant) prés.
5.a. Résoudre l'équation f(x) = g(x)
5.b. Déterminer pour quelles valeurs de x la courbe Cf de la fonction f est située en dessous de, ou sur, la courbe Cg de la fonction g.
6.a. Donner une écriture simplifiée de f(x) / g(x)
6.b. En déduire pour quelles valeurs de x le rapport entre les ordonnées des points M(x;f(x)) et N(x;g(x)) est supérieur ou égal à 1.
Je vous remercie par avance à l'aide que vous pourriez m'apporter,
Raiko
Voici l'exercice :
Les deux fonctions f et g sont définies par : f(x)= (-2x -1)² - (-x+3)²
g(x)= x²-16-(2x+8)(-2x+1).
1. Développer, réduire et ordonner f(x)
2. Factoriser f(x) et g(x)
3.a. Quels sont les antécédents de -8 par f ?
3.b. Pour quelles valeurs de x l'expression f(x) est-elle négative ou nulle?
3.c. Déterminer l'intervalle sur lequel la courbe de la fonction g est située strictement en dessous de l'axe des abscisses.
4. Soit a= racine de 2 / racine de 2+1 (je ne sais pas comment on fait les racines désolé)
Ecrire a avec un dénominateur entier.
Calculer f(a) et en donner une valeur arrondie à 10-1 (-1 est en exposant) prés.
5.a. Résoudre l'équation f(x) = g(x)
5.b. Déterminer pour quelles valeurs de x la courbe Cf de la fonction f est située en dessous de, ou sur, la courbe Cg de la fonction g.
6.a. Donner une écriture simplifiée de f(x) / g(x)
6.b. En déduire pour quelles valeurs de x le rapport entre les ordonnées des points M(x;f(x)) et N(x;g(x)) est supérieur ou égal à 1.
Je vous remercie par avance à l'aide que vous pourriez m'apporter,
Raiko
Alors oui excusez moi j'ai oublié de vous dire ce que j'avais fait donc voici :
f(x) = (-2x-1)² - (-x+3)²
= (-2x-1 +x -3) (-2x-1 -x+3)
= (-x-4) (-3x +2)
Le probleme c'est qu'à la seconde question on nous demande de factoriser f(x) mais c'est ce que je viens de faire...
Aprés je ne comprend plus rien à l'exercice...
f(x) = (-2x-1)² - (-x+3)²
= (-2x-1 +x -3) (-2x-1 -x+3)
= (-x-4) (-3x +2)
Le probleme c'est qu'à la seconde question on nous demande de factoriser f(x) mais c'est ce que je viens de faire...
Aprés je ne comprend plus rien à l'exercice...
1. Développer, réduire et ordonner f(x)
2. Factoriser f(x) et g(x)
Développer n'est pas du tout factoriser sauf preuve du contraire :marteau:
Aller petite aide :
Tu as =(-2x-1)^2 - (-x+3)^2) on te demande de la développer donc tu fais ton calcul et à la fin tu dois obtenir ceci
on te demande de la développer donc tu fais ton calcul et à la fin tu dois obtenir ceci
 = 3x^2 +10x-8) .
.
Ensuite pour Factoriser f(x) cest assez simple il suffit de voir l'identité remarquable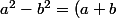(a-b)) a toi de jouer
a toi de jouer
De meme pour g(x), tu as = x^2-16-(2x+8)(-2x+1))
Tu as juste as factoriser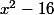 de l'égalité ( pense a utiliser l'identité remarquable que je viens de te donner )
de l'égalité ( pense a utiliser l'identité remarquable que je viens de te donner )
Pour la question 3 les antécédants de -8 sont les nombres qui ont pour image -8 par la fonction f
2. Factoriser f(x) et g(x)
Développer n'est pas du tout factoriser sauf preuve du contraire :marteau:
Aller petite aide :
Tu as
Ensuite pour Factoriser f(x) cest assez simple il suffit de voir l'identité remarquable
De meme pour g(x), tu as
Tu as juste as factoriser
Pour la question 3 les antécédants de -8 sont les nombres qui ont pour image -8 par la fonction f
nxthunder a écrit:1. Développer, réduire et ordonner f(x)
2. Factoriser f(x) et g(x)
Développer n'est pas du tout factoriser sauf preuve du contraire :marteau:
Aller petite aide :
Tu ason te demande de la développer donc tu fais ton calcul et à la fin tu dois obtenir ceci
.
Ensuite pour Factoriser f(x) cest assez simple il suffit de voir l'identité remarquablea toi de jouer
De meme pour g(x), tu as
Tu as juste as factoriserde l'égalité ( pense a utiliser l'identité remarquable que je viens de te donner )
Pour la question 3 les antécédants de -8 sont les nombres qui ont pour image -8 par la fonction f
Alors tout f'abord merci pour cette aide, voilà ce que j'ai fais :
f(x)= (4x²-4x+1)-(x²+3x+9)
= 3x²-7x-8 (donc je ne trouve pas pareil que toi...)
factoriser f(x) :
f(x) = (-2x-1)² - (-x+3)²
= (-2x-1 +x -3) (-2x-1 -x+3)
= (-x-4) (-3x +2)
Factoriser g(x) :
g(x) = (x+4)(x-4) -2(x+4)(-2x+1)
= (x+4) [(x-4) -2(-2x+1)]
= (x+4) (x-4 +4x-2)
= (x+4) (5x-6)
Dites moi si je me trompe s'il-vous-plait.
Par contre je ne comprend pas comment procéder à la question 3 malgré ton aide...
Merci d'avance
Raiko a écrit:Euh ce n'est pas plutot x< ou égal?
Si
et si
Raiko a écrit:ps : comment met-on les inférieurs ou égals, les racines etc...?
Racine carré de x [TEX] \sqrt {x} [/TEX ]
x est inférieur ou égal à 0 [TEX] x \le 0 [/TEX ]
x est supérieur ou égal à 0 [TEX] x \geq 0 [/TEX ]
Sans mettre l'espace entre le "X" et le "]" de [/TEX ]
Raiko a écrit:Euh ce n'est pas plutot x< ou égal?
Si
et si
Raiko a écrit:ps : comment met-on les inférieurs ou égals, les racines etc...?
Racine carré de x [TEX] \sqrt {x} [/TEX ]
x est inférieur ou égal à 0 [TEX] x \le 0 [/TEX ]
x est supérieur ou égal à 0 [TEX] x \geq 0 [/TEX ]
Sans mettre l'espace entre le "X" et le "]" de [/TEX ]
35 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
