Fonctions

par **nada-top** » 05 Sep 2006, 21:42

ben en voyant la suite de l'exo c'est ce qui est demandé de prouver la stricte monotonie !?

par **nox** » 05 Sep 2006, 21:43

ba non ^^

ca me ferait mal en tout cas :p

par **nada-top** » 05 Sep 2006, 21:44

faut faire le tableau de variations et montrer la continuité

C une fonction polynomiale donc elle continue sur R :doh:

par **nox** » 05 Sep 2006, 21:44

nox a écrit:juste dire qu'elle est continue (fonction polynômiale) et monotone (prouvé avant)...

I agree :we:

par **nada-top** » 05 Sep 2006, 21:46

mais pourquoi tu dis ''faire....et montrer la continuité''?!

par **nada-top** » 05 Sep 2006, 21:55

en tous cas pour que Kinou56 comprend la relation entre la bijectivité et l'unicité de la racine , c simple : si

est bijective , on a

alors

donc 0 admet un antécédent unique par la fonction g , c-à-d l'équation g(x)=0 admet une unique solution .

par **nox** » 05 Sep 2006, 22:03

nada-top a écrit:mais pourquoi tu dis ''faire....et montrer la continuité''?!

ba faut les 2...la continuité et le tableau de variation...

mais c'est vrai que la continuité se voit dans le tableau si c'est ce que tu veux dire ^^

ceci dit dans ce cas faut quand meme le préciser c'est important

par **nada-top** » 05 Sep 2006, 22:10

sauf erreur cet équation admet 3 solutions réelle :lol5:

en calculant le descriminant de Cardan je trouve

---négatif donc l'équation admet trois solutions réelle ce qui prouve la fausseté de l'énoncé.

par **nox** » 05 Sep 2006, 22:15

ca me parait bizarre ca voudrait dire qu'on tend vers le meme coté de 0 en - l'infini et en + l'infini

alors que c'est pas le cas

et en faisant le tableau de variations on n'en trouve qu'un je crois...(de tete c'est pas évident ^^)

par **nox** » 05 Sep 2006, 22:21

je confirme il n'y en a qu'un :

démonstration (à rédiger proprement hein...c'est pas noel non plus :p) :

la fonction est continue.

de plus elle est croissante de -infini à -1 et de 1 à +infini (dérivée + étude de signe) et décroissante entre -1 et 1

Or f(-1)<0 (f(-1) = -1) et f(1)<0 (f(1) = -5)
f(+infini) = +infini

donc la fonction coupe l'axe des abscisses une seule fois,et l'abscisse de ce point est entre 1 et l'infini

voilou...

EDIT : je sens venir le post (pour confirmer cette version j'espere) de rene38

par **rene38** » 05 Sep 2006, 22:25

Bonsoir
Confirmation graphique :

par **nox** » 05 Sep 2006, 22:26

CQFD merci rene38

j'aurai du indiquer le timing de mon EDIT dans le post précédent :p

par **nada-top** » 05 Sep 2006, 22:35

désolée le Delta est positif (

)donc elle admet bien une unique solution réelle :lol5:

par **nada-top** » 05 Sep 2006, 22:53

alors maintenant pour trouver une approximation de la racine il faut s'enservir d'un algorithme de recherche du zero , je propose faire une bissection (dite dichotomie) et s'enservir du TVI.

alors un point de départ: on a

et

donc

et

sont de signe opposé et selon le TVI on peut en déduire que

.
-maintenant le centre de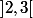

détermine 2 intervalles

et

donc soit

ou

, or on

donc

et

sont de signe opposé ie

..
- idem le centre de

détrmine

et

, faut maintenant trouver le signe de

pour déterminer une autre aproximation de

...et ainsi de suite jusqu'à trouver l'encadrement qu'on cherche.

il ya aussi la méthode de Newton c plus directe mais je crois pas que ça se voit en Terminal .

PS: enfin nada-top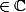

:lol5:

par **kinou56** » 06 Sep 2006, 13:33

je n'ai absolument jamais entendu parler de bissection je ne comprends absolument rien au dernier post.

Pourquoi la fonction est continue. A partir de quoi on peut dire ça stp.

merci pour toutes vos réponses

par **nada-top** » 06 Sep 2006, 13:42

Pourquoi la fonction est continue. A partir de quoi on peut dire ça stp.

ben parce que c'est une fonction polynomiale donc elle est continue sur R .

et pour la bissection ce n'est qu'une application du TVI (théorème des valeurs intermédiaires ) tu le connais ?

par **nox** » 06 Sep 2006, 13:44

kinou56 a écrit:je n'ai absolument jamais entendu parler de bissection je ne comprends absolument rien au dernier post.

Pourquoi la fonction est continue. A partir de quoi on peut dire ça stp.

merci pour toutes vos réponses

ta fonction est un polynôme de degré 3... et on sait que les fonctions polynômiales sont continues. On peut le montrer en disant que la somme/produit/composée de fonctions continues est continue.

Pour la bissection ou dichotomie le principe est le suivant.

on sait qu'en un point x1 la fonction est négative, et qu'en un point x2, avec x2>x1 elle est positive.
Donc comme la fonction est continue, elle est forcément passée par 0 entre x1 et x2.
Alors on regarde maintenant le signe de (x1+x2)/2 (le milieu de l'intervalle [x1, x2]) si c'est positif, la fonction s'annule entre x1 et (x1+x2)/2, sinon elle s'annule entre (x1+x2)/2 et x2...on a ainsi réduit notre intervalle de moitié...et on continue ainsi jusqu'à avoir une valeur aussi approchée qu'on veut du point de passage par 0.

par **kinou56** » 06 Sep 2006, 14:09

non nada-top, je ne l'ai pas encore vu.

par **nox** » 06 Sep 2006, 14:11

on n'en a pas besoin rigoureusement on peut comprendre intuitivement :happy2:

tu as compris mon post au dessus ?

en fait le théorème des valeurs intermédiaires dit si f est continue dans [a;b], alors, pour tout réel k compris entre f(a) et f(b), il existe au moins un réel c de [a;b] tel que f(c)=k .

par **kinou56** » 06 Sep 2006, 14:14

je ne comprends pas à partir du moment où tu parles du signe. dsl

Fonctions

Qui est en ligne