DM Fonctions sec

[Zyrito]

Bonjour, je suis actuellement en seconde, l'année dernière j'ai eu un professeur qui aime la grève. Donc les leçons censées faire n'étaient pas acquises. ce pour quoi je fais une demande d'aide sur ce forum. Je vous en remercie Je ne cherche pas à me faire macher le travail je veux juste comprendre l'exercice.

Voici le DM --->
Voici le lien si l'image ne charge pas http://prntscr.com/pq6kyx (screen pris avec lightshot)
Cordialement

[hdci]

Bonjour,

Pour la question 1), ce n'est pas mathématique mais dessin, une bonne règle graduée en cm et des crayons de couleur devraient suffire (avec une lecture attentive de l'énoncé).

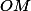
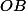
Pour la question 2), il faut compléter le tableau pour des valeurs particulière de , donc de . On sait que le triangle rectangle est isocèle donc on connaît ; avec l'énoncé, on connaît exactement la valeur de donc on en déduit : jusque là il n'y a rien de complexe et même sans avoir eu de cours de maths l'an dernier tu devrais t'en sortir.
Si tu n'arrives pas à "voir" ces calculs, appuie-toi sur des dessins, comme les deux faits lors de la question 1 (et mesurer avec la règle pour comprendre ce qui se passe ; attention une mesure avec la règle n'est pas une preuve mais permet de comprendre ce qu'il faut faire).

Pour calculer l'aire du triangle OMN, tu n'as besoin que d'une seule formule : celle qui donne l'aire d'un triangle rectangle : la connais-tu ? (plus généralement l'aire d'un triangle quelconque ?)

Pour la question 3 : est une variable, c'est-à-dire représente autant de nombres possibles que le permet le contexte de l'énoncé ; le tableau de la question 2 a donné des exemples de valeurs de : 1, 2, 3, 4, 5 et 6. Quand on dit "à intervalle appartient ", il faut trouver quelle est la plus petite valeur que peut prendre , et la plus grande valeur, et s'assurer que peut prendre toutes les valeurs possibles entre ces deux extrêmes. Puis on l'écrit avec le formalisme que tu as dû voir en cours (cette année, pas l'an dernier).
La suite de la question est exactement ce qui a été fait à l'exercice 2, en remplaçant les "cas particuliers" par .

Pour la question 4 : cela se déduit de la question 3 : tu as trouvé la formule qui donne l'aire en fonction de et l'énoncé te dis que est la fonction qui a associe l'aire... Placer les points sur un graphique est simplement appliquer ce que tu as dû voir (cette année en seconde) en terme de courbe représentative d'une fonction (où se trouvent les antécédents, les images... Astuce : "antécédent" commence par la lettre a, tout comme "abscisse").

La question 5 n'est qu'une résolution graphique : autrement dit, comment détermine-t-on le ou les antécédents d'un nombre par une fonction ; là aussi c'est du cours de seconde.