On te demande d'abord de factoriser g(x) en mettant a^n en facteur. C'est une indication très claire.
g(x) = a^n multiplié par quoi ? Tu bloques là-dessus , ou tu sais faire ?
Ensuite, pareil, l'énoncé de l'exercice te guide de façon très précise. Ce n'est peut-être pas flagrant pour l'instant, mais quand tu auras répondu à la question a), tu devrais voir une analogie très claire entre g(x) et la 1ère partie de l'exercice.
Fonctions polynômes
30 messages
- Page 2 sur 2 - 1, 2
Re: Fonctions polynômes
Je ne vois pas très bien :
g(x) = x^n - a^n
g(x) = a^n ( x^n / a^n - 1 )
C'est ça ?
g(x) = x^n - a^n
g(x) = a^n ( x^n / a^n - 1 )
C'est ça ?
Re: Fonctions polynômes
Bonjour ;
Tu peux continuer maintenant en remarquant que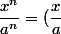^n) .
.
RENE90 a écrit:Je ne vois pas très bien :
g(x) = x^n - a^n
g(x) = a^n ( x^n / a^n - 1 )
C'est ça ?
Tu peux continuer maintenant en remarquant que
Re: Fonctions polynômes
Donc :
g(x) = a^n ( x^n / a^n - 1 )
g(x) = a^n ( x / n - 1 ) [ ( x / a )^n - 1 + ( x / a)^n - 2 + .... = ( x / a )^2 + x / a + 1
C'est ça ?
g(x) = a^n ( x^n / a^n - 1 )
g(x) = a^n ( x / n - 1 ) [ ( x / a )^n - 1 + ( x / a)^n - 2 + .... = ( x / a )^2 + x / a + 1
C'est ça ?
Re: Fonctions polynômes
Je constate une erreur de frappe dans l'expression de g(x) :
Remplacer le signe " = " avant ( x / a )^2 par un signe " + "
Remplacer le signe " = " avant ( x / a )^2 par un signe " + "
Re: Fonctions polynômes
Oui , c'est cà .
Il faut juste rectifier ces fautes de frappe .
Il faut juste rectifier ces fautes de frappe .
RENE90 a écrit:Donc :
g(x) = a^n ( x^n / a^n - 1 )
g(x) = a^n ( x/a - 1 ) [ ( x / a )^n - 1 + ( x / a)^n - 2 + .... + ( x / a )^2 + x / a + 1
C'est ça ?
Re: Fonctions polynômes
OK, je suis content, grâce à toi, d'arriver à quelque chose !
Mais comment faire apparaître maintenant le facteur x - a ?
Mais comment faire apparaître maintenant le facteur x - a ?
Re: Fonctions polynômes
OK parfait !
Il y a encore une dernière question mais je pense pouvoir me débrouiller seul
Encore merci pour ton aide !
Il y a encore une dernière question mais je pense pouvoir me débrouiller seul
Encore merci pour ton aide !
30 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 109 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
