Fonctions dérivables

[haricot29]

:hum: Voila mon prof de maths a voulu a tout prix finir le cours sur le chapitre de dérivation avant les vacances sachant qu'on la commencé mardi donc on a fait ça en 5h. On a fait aucuns exo on a fait que copié du cours et pour les vacs il nous a donné une 15aine d'exos a faire...

Le probleme c'est que je n'ai mais alors rien compris ! Donc si quelqu'un pouvait me donné un petit coup de pouce o moins sur le 1er exo ! Merci

Consigne : Pour les exos suivants, calculer f ' (x) en précisant pour quelles valeurs votre calcul est valable.

exo n° 1
f(x) = -5x^3 +4x² -9x -5
f(x) = -(1/2)x^4 +3x^3 -4x² + (racine de 3)*x +1

Voila qui vous pouvez m'aider ce serait vachement simpa !

[Anonyme]

pour derivé un terme en x^(quelque chose lol) tu descend lexposan d 1 et tu multipli la constante par lexposant du debu exempl
f(x)=5x^8+3x^5-7x^3+6x²-4x+6

alors on a :
f'(x)=5*8x^(8-1)+3*5x^(5-1)-7*3x^(3-1)+6*2x^(2-1)-4*1x^(1-1)+6*0
=40x^7+15x^4-21x²+12x-4

tu pourra remarker k quand "il n'y a pas de x" c'est egale a zero(c'est du a l'exposant zero du x )

[Anonyme]

voila en esperant t'aider un peu .

[Zebulon]

Bonjour,
je suppose que tu sais que la dérivée d'une somme est la somme des dérivées.
Par ailleurs, que vaut la dérivée d'une fonction constante , avec un réel quelconque?
De plus, connais-tu la dérivée de la fonction définie sur par , où a est un réel quelconque? C'est , définie sur . Le domaine de définition de la fonction dérivée f' est le domaine de dérivation de la fonction f.
Enfin, soit la fonction , avec un réel quelconque et f une fonction dérivable sur un certain domaine, alors g est dérivable sur le même domaine de dérivation que f et sa dérivée vaut .
Alors, quels sont le domaine de définition, la dérivée et le domaine de dérivabilité de la fonction , où , , a et b sont des réels quelconques?
Si tu as compris ça, tu sauras faire tes exercices.
Bon courage et n'hésite pas à poser des questions si tu ne comprends pas :++: .
A bientôt,
Zeb.

[haricot29]

donc si j'ai bien compris pour :
f(x) = -5x^3 + 4x² - 9x - 5
f ' (x) = -15x² + 8x -4 ???

Merci de me dire si c'est bon ?!

[S@m]

Heu non pourquoi -4?

La dérivée d'un polynome est la somme des dérivées, or la dérivée de -5 est nulle et celle de -9x est égal a -9 :happy2:

Donc au final:

f '(x)= -15x² + 8x -9.

[haricot29]

oui c'est -9 une erreur de recopiage !

et pour celle-ci c'est bon :
f(x) = -(1/2)x^4 + 3x^3 - 4x² + (racine de 3)*x + 1
f ' (x) = -2x^3 + 6x² - 8x + (racine de 3)

Merci de me dire si c'est bon ?!

[S@m]

Attention c'est:


f ' (x) = -2x^3 + 9x² - 8x + (racine de 3)
:++:

Et si le moins devant (1/2)x^4 est bien hors de la parenthèse alors oui c 'est bon :happy2:

[haricot29]

:hein: quelqu'un peut-il me confirmer mes résultats ?! Me dire s'ils sont OK ?!

a) f(x) = ((racine de 3) -1)x² + 3x - pi
f ' (x) = 2((racine de 3) -1)x +3

b) f(x) = -(racine de x) + x²/2
f ' (x) = x

c) f(x) = (x-2) * (racine de x)
f ' (x) = (racine de x) + (x-2)/(2*(racine de x))

PS : Merci S@m de me rep et de m'aider c'est simpa de ta part !

[rene38]

Bonjour

Attention : si alors

[rene38]

Bonjour

Attention : si alors à utiliser dans b)

[quinto]

ca me semble faux rené.
A+

[haricot29]

ah bon ! je ne veux pas dire que ce que tu dis la est faux mais dans mon livre il y a un exo corriger ou quand f(x) = racine de X il est marquer que f ' (x) = 1 / 2 * racine de X

donc est-ce que tu as fait un faute involontaire en mettant un moins devant le résultat ou alr est ce que c'est dans mon bouquin qu'ils se sont trompés ?
MERCI

[rene38]

Non, tu as (vous avez) raison : erreur de ma part, corrigée.

Mais ton b) me semble faux tout de même : tu n'as pas dérivé .

[haricot29]

d'accord merci, personnelement ça ne me gene pas du tout que tu me tutoie je t'ai tutoyer d'abord j'espere que cela ne ta pas déranger !

[rene38]

d'accord merci, personnelement ça ne me gene pas du tout que tu me tutoie je t'ai tutoyer d'abord j'espere que cela ne ta pas déranger !

Je VOUS tutoie : je répondais à 2 personnes ... : haricot29 et quinto.

[haricot29]

celle-ci sont-elles correctes ?

a) f(t) = 4t^5 / 5
f ' (t) = 0

b) f(x) = (x^3 + 12x -1) / 4
f ' (x) = (-x^3 + 3x² + 12x - 11) / 4

c) f (u) = ( 2u + 3 ) ( 5u + 1)
f ' (u ) = 20u +17

[Zebulon]

Les a et b ne sont pas bonnes. Comment as-tu trouvé ça??? Revoie bien les calculs des dérivées de polynômes.
Zeb.

[haricot29]

alors pour :
a) f(t) = 4t^5 / 5
f ' (t) = 0

j'ai fait a partir d'un exemple de mon boukin :
f(t) = 4t^5 / 5
u : t --> 4t^5
v : t --> 5

u ' : t --> 20t^4
v ' : t --> 5
f (u/v) ' = ( u'v - uv')/v²
dc j'ai fait le calcul avec mé resultat et je trouve f ' (t) = 0

-------------------------------------------------------------------------

pour :
b) f(x) = (x^3 + 12x -1) / 4
f ' (x) = (-x^3 + 3x² + 12x - 11) / 4

u : x --> x^3 + 12x -1
v : x --> 4

u' : x --> 3x² + 12
v' : x --> 4

f '(x) = (u'v) - ( uv')
et avec mes résultats j'ai trouvé : f ' (x) = (-x^3 + 3x² + 12x - 11) / 4

[Zebulon]

OK, alors pour la a:
tu as considéré que était une fonction de t. Pourquoi pas? Dans ce cas, c'est ce qu'on appelle une fonction constante. Que vaut donc sa dérivée? D'autre part, tu peut voir la fonction sous un autre angle, plus simple pour la dérivation: et maintenant tu dérives avec comme constante. Essaie les deux méthodes, ça ne peut que t'entraîner (même si j'insiste, c'est la deuxième la plus efficace).
Après avoir corrigé la a, vois-tu ton erreur dans la b?
Zeb.
PS: ATTENTION!!! la dérivée de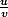 est . N'oublie pas de mettre le dénominateur au carré!