Fonctions continues
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
amed61
- Membre Naturel
- Messages: 20
- Enregistré le: 19 Sep 2012, 20:32
-
 par amed61 » 14 Oct 2013, 15:43
par amed61 » 14 Oct 2013, 15:43
exo1
et

deux fcts définies et continues de

vers

, telles que pour tout

de

on a :
=gof(x))
montrer qu'il existe au moins un nombre c de

tel que:
 = g(c)) Exo2
Exo2
une fct continue de

vers

et telle que
=f(1))
pour tout entier naturel non nul n on pose:
 = f(x+\frac{1}{n})-f(x))
Montrer que pour tout n l'équation
=0)
admet une solution dans lintervalle
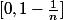

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 14 Oct 2013, 16:31
par chombier » 14 Oct 2013, 16:31
amed61 a écrit:exo1
f et g deux fcts définies et continues de [0,1] vers [0,1], telles que pour tout x de [0,1]on a : fog(x)=gof(x)
montrer qu'il existe au moins un nombre c de [0,1] tel que: f(c) = g(c)
Exo2
f une fct continue de [0,1] vers [0,1]
pour tout entier naturel non nul n on pose: gn(x) = f(x+1/n)-f(x)
Montrer que pour tout n l'équation gn(x)=0 admet une solution dans lintervalle [0,1-1/n]
Ça sens fort le théorème des valeurs intermédiaires et son corollaire.
-
amed61
- Membre Naturel
- Messages: 20
- Enregistré le: 19 Sep 2012, 20:32
-
 par amed61 » 14 Oct 2013, 16:48
par amed61 » 14 Oct 2013, 16:48
chombier a écrit:Ça sens fort le théorème des valeurs intermédiaires et son corollaire.
Oui pour ce là j'ai considéré la fct h(x) = f(x) - g(x) pour l'exo1 mais j'arrive pas à trouver a et b tels que h(a)*h(b) <0
-
tototo
- Membre Rationnel
- Messages: 954
- Enregistré le: 08 Nov 2011, 07:41
-
 par tototo » 15 Oct 2013, 10:56
par tototo » 15 Oct 2013, 10:56
amed61 a écrit:exo1
f et g deux fcts définies et continues de [0,1] vers [0,1], telles que pour tout x de [0,1]on a : fog(x)=gof(x)
montrer qu'il existe au moins un nombre c de [0,1] tel que: f(c) = g(c)
Exo2
f une fct continue de [0,1] vers [0,1]
pour tout entier naturel non nul n on pose: gn(x) = f(x+1/n)-f(x)
Montrer que pour tout n l'équation gn(x)=0 admet une solution dans lintervalle [0,1-1/n]
Bonjour
montrons que gn(0)*gn(1-1/n)<0 et que gn(x) est monotone (croissante si f l'est decroissante selon f)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Oct 2013, 13:40
par chan79 » 15 Oct 2013, 13:40
salut
f étant continue, il existe un a de [0;1] tel que f(a)=a
ensuite essaie par l'absurde:
S'il n'avait pas de c tel que f(c)=g(c), comme f-g est continue, on aurait toujours:
f(x)g(x)
on peut supposer f(x)<g(x)
ensuite
)=g(f(a))=g(a))
)
est invariant par

on pose
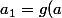)
)=g(f(a_1))=g(a_1))
)
est invariant par f
on pose
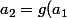)
etc
Etudie la suite


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Oct 2013, 09:10
par chan79 » 16 Oct 2013, 09:10
amed61 a écrit:
[B]Exo2
f une fct continue de [0,1] vers [0,1]
pour tout entier naturel non nul n on pose: gn(x) = f(x+1/n)-f(x)
Montrer que pour tout n l'équation gn(x)=0 admet une solution dans lintervalle [0,1-1/n]
salut
si on prend
=x)
=x+\fra{1}{n}-x=\fra{1}{n})
ne s'annulle jamais
-
keofran
- Membre Relatif
- Messages: 125
- Enregistré le: 12 Oct 2013, 00:39
- Localisation: Lyon
-
 par keofran » 16 Oct 2013, 22:30
par keofran » 16 Oct 2013, 22:30
Sympa la méthode, j'ai réfléchi un moment sans trouver.
-
amed61
- Membre Naturel
- Messages: 20
- Enregistré le: 19 Sep 2012, 20:32
-
 par amed61 » 18 Oct 2013, 19:29
par amed61 » 18 Oct 2013, 19:29
chan79 a écrit:salut
f étant continue, il existe un a de [0;1] tel que f(a)=a
ensuite essaie par l'absurde:
S'il n'avait pas de c tel que f(c)=g(c), comme f-g est continue, on aurait toujours:
f(x)g(x)
on peut supposer f(x)<g(x)
ensuite
)=g(f(a))=g(a))
)
est invariant par

on pose
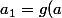)
)=g(f(a_1))=g(a_1))
)
est invariant par f
on pose
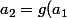)
etc
Etudie la suite

la suite

est croissate et majorée donc elle a une limite l
Et l est invariante par f et g

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 18 Oct 2013, 19:38
par chan79 » 18 Oct 2013, 19:38
amed61 a écrit:la suite

est croissate et majorée donc elle a une limite l
Et l est invariante par f et g
oui, et on avait supposé qu'il n'y avait pas de c tel que f(c)=g(c)
or f(l)=g(l)=l
-
amed61
- Membre Naturel
- Messages: 20
- Enregistré le: 19 Sep 2012, 20:32
-
 par amed61 » 18 Oct 2013, 19:41
par amed61 » 18 Oct 2013, 19:41
amed61 a écrit:la suite

est croissate et majorée donc elle a une limite l
Et l est invariante par f et g
Je me suis inspiré pour l'exo 2
Je procède par absurde, je suppose que gn ne s'annule jamais sur l'intervale [0,1-1/n]
Donc elle est soit strict positive soit strict négative (je suppose <0)
Ansi je vais avoir:
<f(o))
<f(\frac{1}{n}))
.......
<f(\frac{n-2}{n}))
<f(\frac{n-1}{n}))
en additionnant on obtient
<f(0))
ce qui est absurde

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 18 Oct 2013, 22:16
par chan79 » 18 Oct 2013, 22:16
amed61 a écrit:
[B]Exo2
une fct continue de

vers

pour tout entier naturel non nul n on pose:
 = f(x+\frac{1}{n})-f(x))
Montrer que pour tout n l'équation
=0)
admet une solution dans lintervalle
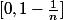
Salut
problème d'énoncé, je pense
avec f(x)=x,
=\fra{1}{n})
qui ne s'annulle pas

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 18 Oct 2013, 22:21
par chan79 » 18 Oct 2013, 22:21
amed61 a écrit:Exo2
une fct continue de

vers

pour tout entier naturel non nul n on pose:
 = f(x+\frac{1}{n})-f(x))
Montrer que pour tout n l'équation
=0)
admet une solution dans lintervalle
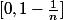
attention, ça doit être
 = f(\fra{x+1}{n})-f(x))
car sinon, avec f(x)=x c'est visiblement faux
-
amed61
- Membre Naturel
- Messages: 20
- Enregistré le: 19 Sep 2012, 20:32
-
 par amed61 » 21 Oct 2013, 09:26
par amed61 » 21 Oct 2013, 09:26
chan79 a écrit:attention, ça doit être
 = f(\fra{x+1}{n})-f(x))
car sinon, avec f(x)=x c'est visiblement faux
Ah! oui j'ai oublié une condition dans l'énoncé qui est:
=f(1))
-
besttrainer
- Membre Naturel
- Messages: 32
- Enregistré le: 09 Juil 2013, 22:15
-
 par besttrainer » 21 Oct 2013, 12:57
par besttrainer » 21 Oct 2013, 12:57
salut ! je n'arrive pas à résoudre le premier exo et j'ai vu que vous avez parlé de créer une suite
est ce que vous pouvez méclaircir ce point en détailles :we: ??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
est invariant par
est invariant par f
est croissate et majorée donc elle a une limite l