Fonctions bornées (Maths)

[eclipse75]

Bonsoir tout le monde,
voila, j'ai un problème pour mes exercices de maths que voici:

1) Résoudre:

|x|=7
|2x+1|=2
|2-3x|=|x+5|
|3x+2|=-3
|x||x|>ou=Pi
|x|>ou=-2
|4x-3||6x+1|>4


2) Compléter:

|x| = alpha <=> ...
|x| ...
|x| >ou= alpha <=> ...

Justifier.

Quelqu'un peut m'aider s'il vous plaît?
Merci d'avance ..

[Ericovitchi]

Dès que tu es devant des valeurs absolues, il faut te soucier du signe de ce qu'il y a à l’intérieur de façon à être en mesure de les enlever et donc de revenir à des équations traditionnelles.

Donc prenons un de tes exemples. |2x+1|=2
2x+1 c'est positif si x >-1/2 et négatif sinon donc
x<-1/2 --> |2x+1| = -2x-1 et
x>-1/2 --> |2x+1| = 2x+1
il te reste à résoudre dans chaque cas |2x+1|=2, à vérifier si la solution obtenue est bien dans l'intervalle de départ ou pas, si oui tu retiens la solution, sinon non.

C'est le principe à appliquer pour tous les cas que tu as à résoudre.

[eclipse75]

Merci pour votre aide, j'ai pu résoudre les éaquations/inéquations,

Mais maintenant, le problème c'est pour l'exercice 2)

Je sais que:

|x| = ;) <=> x = ;) ou bien x = - ;)

|x| ;) ;) <=> x ;) ;) ou bien x ;) - ;)

|x| ;) ;) <=> x ;) ;) ou bien x ;) - ;)

mais comment le justifier ? :hein:

Je vous remercie d'avance

[Ericovitchi]

Comment justifier ?

|x| = c'est que x²=a² donc x²-a²=0 donc (x-a)(x+a)=0 donc x = + ou - a

|x| c'est x²;) a² donc x²-a²;) 0 un polynôme du second degré est du signe de son terme de plus haut degré (donc positif ici) en dehors des racines donc x [-a;+a]

|x| c'est x² a² donc x²-a²;) 0 un polynôme du second degré est du signe de son terme de plus haut degré (donc positif ici) en dehors des racines donc x [-;-a] U [a;

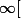
[eclipse75]

Est-tu sure que dans les 2 cas c'est "du signe de son terme de plus haut degré (donc positif ici) en dehors des racines"

Les 2 doivent êtres différents non?

PS: Borne infini toujours ouvert :)