Bonjour, je suis en première S et je n'arrive pas à trouver les solutions d'un exercice faisant partie d'un DNS à rendre. Voici l'énoncé :
Pour chaque affirmation, indiquer si elle est vraie ou fausse en justifiant :
a. Si f et g sont croissante sur un intervalle I, la fonction h définie pour tout x de I par h(x) = f(x)+g(x) est croissante sur I.
b. Si f et g sont décroissante sur I, la fonction h définie pour tout x de I par h(x) = f(x)+g(x) est décroissante sur I.
c. Si f et g sont monotones sur I, la fonction h définie pour tout x de I par h(x) = f(x)+g(x) est monotone sur I.
d. Si f et g sont croissantes sur I, la fonction h définie pour tout x de I par h(x) = f(x)xg(x) est croissante sur I.
Il me semble que le prof avait insinué qu'il fallait chercher des contres-exemples mais c'est là tout le problème, je ne vois pas comment faire. Merci d'avance de votre aide !
Fonctions associées
6 messages
- Page 1 sur 1
Les contre exemples doivent être trouvés quand la réponse est fausse : Il suffit de trouver un et un seul exemple qui ne vérifie pas la propriété proposée pour prouver qu'elle est fausse. En revanche si elle est vraie, il faut le montrer dans le cas général
a. Une fonction est croissante sur I si pour tout (a,b) dans I tel que a0 . Comment adapter ce raisonnement à ta fonction h ?
b. Même raisonnement
c. Il s'agit de trouver un contre'exemple, c'est à dire deux fonctions monotones (c'est à dire toujours décroissante ou toujours croissante) telles que leur somme ne le soit pas
d. même raisonnement que a.
a. Une fonction est croissante sur I si pour tout (a,b) dans I tel que a0 . Comment adapter ce raisonnement à ta fonction h ?
b. Même raisonnement
c. Il s'agit de trouver un contre'exemple, c'est à dire deux fonctions monotones (c'est à dire toujours décroissante ou toujours croissante) telles que leur somme ne le soit pas
d. même raisonnement que a.
Tu n'essaies pas de comprendre, fais un effort tout de même
On te dit que :
Une fonction f est croissante sur I si pour tout (a,b) dans I tel que a0
En l'occurence, tu sais que ta fonction f est croissante , ta fonction g aussi, et tu veux montrer que h=f+g est croissante.
Tu sais que, pour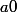 ,
, -g(a)>0) , donc
, donc  - h(a) = f(b)+g(b) - (f(a)+g(a))) ....?
....?
On te dit que :
Une fonction f est croissante sur I si pour tout (a,b) dans I tel que a0
En l'occurence, tu sais que ta fonction f est croissante , ta fonction g aussi, et tu veux montrer que h=f+g est croissante.
Tu sais que, pour
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 100 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
