[Scde] Fonctions affines

[alexdakos]

Salut a tous,

j´ai deux exos a faire pour demain sur les fonctions affines, et je planche totalement, vu que je comprends pratiquement rien aux fonctions :

"Dans cas cas, expliquer pourquoi f ,n´est pas définie sur l´intervalle E donné. Proposer un intervalle I sur lequel f est définie.

a) E = IR et f(x) = 1 / x + 2
b) E = [0 ; + infini[ et f(x) = V(x - 1)

(V signifie racine)

----------------

ABCD est un carré de coté 5.
L , M, P, Q sont respectivement les points des segments [AB], [CD], et [DA] tels que AL = BM = CP = DQ = x
Le quadrilatere LMPQ est un carré.

a) Quelles sont les valeurs possibles de x ?

b) Exprimer PM² en fonction de x
En deduire l´aire de LMPQ

c) On note f la fonction qui associe x à A
Quelle est l´ensemble de definition de cette fonction ?
- Calculer les images par f des réels 0, 1, 2.5, 5

-----------

Serieux je galere vraiment, si vous pouviez me donner au moins un bon indice pour chaque question ...

Merci d´avance

[maturin]

quand tu dis qu'une fonction n'est pas définie en un point x c'est que tu peux pas la calculer avec la formule de f(x).

exemple :
n'est pas définie pour x=0 car 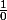n'existe pas.
tu peux donc dire que la fonction f telle que est définie sur R-{0} (l'ensemble des réels moins le point 0).

de même n'existe pas si x est négatif car la racine d'un nombre négatif n'existe pas
tu peux donc dire que la fonction f telle que est définie sur R+ (l'ensemble des réels positifs).


pour l'exercie 2 il faut que tu dise que le points point LMPQ appartiennent au segment et cela veut dire AL0)
pour PM² tu fais un dessin et tu appliques le théroème de pythagore. remarque : si BC=5 et BM=x alors MC=5-x
un fois que tu as la longueur du côté c'est facile d'avoir l'aire du carré.
c) l'ensemble de définition de f c'est l'ensemble des x pour lesquels f est définie hors on a défini le carré et donc son aire pour 0<x<5.

pour le calcul je te laisse faire une fois que tu connais la formule de f il suffit de remplacer x par les valeurs et de calculer.


remarque : il faut interpréter tous mes < comme des inférieurs ou égal

[alexdakos]

Merci enormement :)

En fait ce que je veux surtout savoir pour l'exo 1, c'est ce que veut dire exactement E = IR et E = [0 ; + infini[
E = IR signifie que l'intervalle E est un réel ?

E = [0 ; + infini[ signifie que E > 0 ? pourquoi deux crochets vers la droite ?

[alexdakos]

:up: svp, c'est assez urgent

[alexdakos]

Voila ce que j'ai mis comme réponse aux deux exos, dites moi si y'a des trucs a corriger / inutiles etc... :

1er exo :

a) E = IR
f(x) = 1 / (x + 2)

Si x = -2 (en effet -2 £ IR (£ signifie "est sur")), alors f n'est pas définie dans l'intervalle E car 1 / (-2 +2) = 1 / 0 n'existe pas.

Intervalle I possible : IR+

b) E = [0 ; + infini[
f(x) = V(x - 1)

Si x = 0,5 (en effet 0,5 £ [0 ; + infini[ ), alors f n'est pas définie dans l'intervalle E car V(0,5 - 1) n'existe (une racine ne peut etre négative)

Intervalle I possible : [1 ; + infini[

------------------------------------------------

Exo 2 :

a) L £ [AB]
Donc AL < (sous-entendu inférieur ou égal) AB
Comme AB = 5 et AL = x alors
x < (meme remarque qu'en haut) 5

x est une distance donc x > 0 alors :

0 < x < (" ") 5

x £ [0 ; 5]

b) D'après Pythagore dans le triangle PMC rectangle en C :

PM² = MC² + PC²
PM² = (5 - x)² + x²
PM² = (5 - x + x) (5 - x - x)
PM² = 25 - 10x
Donc Aire LMPQ = 25 - 10x

c) O < x < 5

10 X 0 - 25 < 10x - 25 < 10 X 5 - 25
- 25 < 10x - 25 < 25

d) f(0) = - 25
f(1) = - 15
f(2,5) = 0
f(5) = 25

---------

Voila :) j'espere pas avoir fait de fautes

[maturin]

PM² = (5 - x)² + x²
PM² = (5 - x + x) (5 - x - x)

Ca c'est faut c'est a²-b² qui est égal à (a-b)(a+b) et pas a²+b².
ça remet en cause les questions qui suivent mais sinon dans l'esprit c'était ça.
En plus si tu corriges tu verras que t'auras plus d'aires négatives ce qui est fort heureux :happy2:

Sinon quand tu dis que E=R c'est que E est la même chose que R
E est un ensemble et ce n'est pas un point unique. C'est l'ensemble de définition de f. Enfin quand tu a mis E=R+ ou E=[1,+inf[ c'est correct car ce sont bien des ensembles.