Fonctions 1ereS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
c0up-de-x3
- Messages: 6
- Enregistré le: 27 Sep 2009, 14:49
-
 par c0up-de-x3 » 27 Sep 2009, 15:06
par c0up-de-x3 » 27 Sep 2009, 15:06
Bonjour j'ai un sujet à rendre pour demain si vous pouviez m'aider cela m'arrangerait.
On donne : la fonction f définie sur IR par f(x) = x^3-3x
1 - Le théorème sur les sommes de fonctions permet-il d'etudier les variations de f ? Justifier .
2 - Montrer que f est impaire . Quelle conclusion peut en tirer?
3 - On désigne par a et b 2 nombres reels . Montrer que ( a - b ) (a² +ab + b² ) = a^3 - b^3 et que (a-b)(a²+ab+b²-3) = f(a) - f(b).
4- Montrer que : 0
0 . Que peut on en conclure?
5- Etudier les variations de f sur [1; +l'infini ]
Pour le 1 Je n'ai aucune idée !
J'ai trouvé pour le 2 : f(x) = x^3-3x
f(-x) = (-x)^3 - (- 3 x) = -x^3+3x = -(x^3-3x) = -f(x)
Pour tout x appartenant à IR , -x appartient à IR donc: f(-x) = -f(x) donc f est impaire.
3- (a-b)(a²+ab+b²)=a^3-b^3
Soit a^3 - b^3 = (a-b)(a+b)(a+b) = (a-b)(a+b)²
On remarque une identité remarquable donc:
a^3-b^3 = (a-b)(a²+2ab+b²)
F(a) = a^3-3a
F(b)=b^3-3b
F(a)-F(b) = (a^3-3a)-(b^3-3b) = a^3-3a- b^3 + 3b
En developpant on retrouve (a-b)(a²+a-b²-3)
Le 4 - On sait que si a
Pouvez vous m'aider pour le reste svp? & confirmer mes reponses assez vite? Merci d'avance.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Sep 2009, 15:26
par Ericovitchi » 27 Sep 2009, 15:26
3- (a-b)(a²+ab+b²)=a^3-b^3 Soit a^3 - b^3 = (a-b)(a+b)(a+b) = (a-b)(a+b)² On remarque une identité remarquable donc: a^3-b^3 = (a-b)(a²+2ab+b²)
c'est assez fantaisiste tout ça
a^3 - b^3 = (a-b)(a+b)(a+b) !!!! vois pas pourquoi
et à la fin tu tombes sur (a-b)(a²+2ab+b²) au lieu de (a-b)(a²+ab+b²) et ça ne te trouble pas plus que ça.
non le mieux est de partir de (a-b)(a²+ab+b²), de faire le produit et de trouver
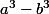
-
c0up-de-x3
- Messages: 6
- Enregistré le: 27 Sep 2009, 14:49
-
 par c0up-de-x3 » 27 Sep 2009, 15:56
par c0up-de-x3 » 27 Sep 2009, 15:56
Si j'ai bien compris je dois faire :
a*(a + ab + b²) et b*(a² + ab + b²)
Ensuite le premier produit moins le deuxieme?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Sep 2009, 16:02
par Ericovitchi » 27 Sep 2009, 16:02
oui.
Effectivement il faut savoir développer une expression algébrique pour résoudre ce genre de problème.
-
c0up-de-x3
- Messages: 6
- Enregistré le: 27 Sep 2009, 14:49
-
 par c0up-de-x3 » 27 Sep 2009, 16:12
par c0up-de-x3 » 27 Sep 2009, 16:12
Ericovitchi a écrit:oui.
Effectivement il faut savoir développer une expression algébrique pour résoudre ce genre de problème.
D'accord merci mais c'est bien du niveau 1ereS si je fais de cette facon?
-
GaRDeLaMe
- Membre Naturel
- Messages: 28
- Enregistré le: 24 Jan 2007, 11:00
-
 par GaRDeLaMe » 27 Sep 2009, 18:18
par GaRDeLaMe » 27 Sep 2009, 18:18
C'est même niveau 3ème ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
