Fonction usuelles et encadrement

[Pouletbraisé]

Bonjour, je dois faire un exercice mais je suis un peu bloqué, je vous donne l'énoncé :
La fonction f est définie sur R par : f (x) =
A. Montrer que pour tout x réel , on a : f (x) =
B. En décomposant f à l'aide des fonctions usuelles, montrer que : f (x) 1/3 quelque soit x
C. Déterminer alors un encadrement de f (x) sur R
Voilà,
J'ai fais la A ,mais je bloque pour la B et la C ...
Si quelqu'un pouvait m'aider

[aviateur]

B. Franchement, je n'ai jamais compris pourquoi dans les exercices on donne des indications si vagues et si perturbantes telles que " En décomposant f à l'aide des fonctions usuelles."
Donc je simplifie la question :"montrer que : f (x) >=1/3 quelque soit x"
Dans ce genre de question un premier réflexe est de calculer et simplifier f(x)-1/3. Essayez.

C. Pour cette question on a grâce à B une minoration. Il faut trouver une majoration. Essayez de deviner
un nombre disons A tel que f(x)<=A , pour tout x. Une fois que vous pensez avoir trouver A montrer
alors que f(x)<=A

[Ben314]

Salut,

B. Franchement, je n'ai jamais compris pourquoi dans les exercices on donne des indications si vagues et si perturbantes telles que " En décomposant f à l'aide des fonctions usuelles."

A mon avis, le "but du jeu", c'est de faire comprendre à l'élève le fait (complètement trivial...) qu'une fois que la formule définissant f(x) ne contient plus qu'une seule fois le symbole , il n'y a plus besoin de faire des calculs pour répondre à bon nombre de questions, mais uniquement à "enquiller" les déductions de proche en proche.

Par exemple, là, je pense que ce qui est attendu, c'est de dire que :
Si on part d'un réel quelconque alors :
- Le réel est positif ou nul (fonction "de référence" ).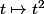
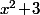
- Le réel est supérieur (ou égal) à 3 (fonction "de référence" ).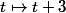
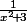
- Le réel est strictement positif et inférieur (ou égal) à (fonction "de référence" )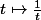
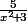
- Le réel est strictement positif et inférieur (ou égal) à 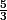(fonction "de référence" ).
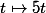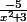
- Le réel est strictement négatif et supérieur (ou égal) à 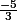(fonction "de référence" ).
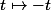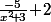
- Le réel est strictement plus petit que et supérieur (ou égal) à 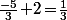(fonction "de référence" ).

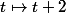Et à mon avis, c'est pas complètement con d'exiger que l'élève procède de la sorte : déjà, ça se fait "de tête" et sans calcul, et ça fait aussi réviser les "fonctions de références" et surtout les inégalités.

Et, toujours à mon avis, c'est pas con du tout dans ce type de contexte (une seul occurrence de ) de demander aussi à l'élève de déterminer les variations de sans effectuer de nouveau calcul (i.e. de nouveau uniquement en composant des "fonctions de référence")

[Pouletbraisé]

D'accord je comprends parfaitement ce que vous venez de faire pour B, mais pour C j'ai un problème, durant notre cours la dessus notre professeur nous as donné que des exercices ou un intervalle étais déjà donné, la c'est sur R que l'on doit chercher
Exemple d'un exercice donné en cours : " f (x) = 3x-3 sur [ 1 ; 3/2 ] , étudier ses variations et donner un encadrement de la fonction "
La on a un intervalle, mais sur l'exercice sur lequel on parle c'est sur R , je ne vois vraiment pas comment procéder. ...

[aviateur]

Bon ici on travaille sur R, autrement dit x est "quelconque", contrairement à vos habitudes.
Pour vous aider, regarder l'expression de f(x) de la question A. Ne voyez vous pas de façon évidente un nombre (disons A) tel que f(x)<A , pour tout x?
Remarque: en général dans ce genre de question, on souhaite que A soit le plus petit possible. Il serait bien de
savoir si ce que vous avez trouver répond à ce critère.

[Pouletbraisé]

Euhhhh, à vrai dire je ne vois pas trop ...

[Pseuda]

D'accord je comprends parfaitement ce que vous venez de faire pour B, mais pour C j'ai un problème. ...

Bonjour,

Si tu as bien suivi la démarche de Ben314, celui-ci a fait les questions B et C en même temps. Tu ne devrais donc pas avoir de problème.

[Pouletbraisé]

Donc pour l'intervalle, x est compris entre 1/3 et 2
Et donc l'encadrement est 11/28 et 9/7 ?

[Emmanuel]

Salut.. Pour ton exo s'il n'était pas question d'utiliser les fonctions usuelles tu pouvais utiliser le théorème de l'inégalité des accroisements finis 1ère formulation. Et tu pourra faire ceci même pour ta 2ème fonction sur l'interval donné .

pour tout x de R est derivable sur R comme rapport de fonction derivable sur R.


Maintenant tu étudies le sens de variations de sur R tu vas voir que pour tout x de R et un encadrement de sera pour tout x de R. Et tu peux maintenant utiliser le théorème de l'inégalité des accroisements finis.
Pour tout 0,x appartenant à R on a d'une part et d'autre part ceci donc d'où le résultat

[Pseuda]

Salut.. Pour ton exo s'il n'était pas question d'utiliser les fonctions usuelles tu pouvais utiliser le théorème de l'inégalité des accroisements finis 1ère formulation. Et tu pourra faire ceci même pour ta 2ème fonction sur l'interval donné .

pour tout x de R est derivable sur R comme rapport de fonction derivable sur R.


Maintenant tu étudies le sens de variations de sur R tu vas voir que pour tout x de R et un encadrement de sera pour tout x de R. Et tu peux maintenant utiliser le théorème de l'inégalité des accroisements finis.
Pour tout 0,x appartenant à R on a d'une part et d'autre part ceci donc d'où le résultat

Bonjour,

Joyeux mélange. Comment une valeur absolue peut-elle être strictement négative ?

[Pseuda]

Donc pour l'intervalle, x est compris entre 1/3 et 2
Et donc l'encadrement est 11/28 et 9/7 ?

Bonjour,

Non x appartient à R, et c'est f(x) qui est compris entre 1/3 et 2. Si tu n'en est pas convaincu, affiche le graphe de la fonction avec ta calculatrice.

[Ben314]

Joyeux mélange. Comment une valeur absolue peut-elle être strictement négative ?

Sans parler du fait que l'énoncé demande explicitement de le faire par compositions de "fonction élémentaires" donc surement pas en étudiant le signe de la dérivée (*).
Sans parler du fait qu'à mon avis c'est un exercice de seconde et que les dérivées n'ont pas étés abordées à ce niveau là.

(*) Et je (re)précise ce que j'ai déjà dit ci dessus : pour une fois qu'il y a un exo. qui demande à "comprendre" comment on "décortique" une fonction pour en tirer de l'info. sans calculs supplémentaires, ben je trouve ça très très con d'inciter l'élève à se comporter comme un "no brain" (par exemple en l'incitant à calculer la dérivée alors qu'on peut trouver les variations sans le moindre calcul mais uniquement avec du raisonnement)

[Pouletbraisé]

Euhhhh.. Ducoup je dérive ou je dit juste que la solution est 1/3 et 2 ,... vous m'avez perdu la

[Pseuda]

Si tu as bien suivi, pour faire l'exercice, il ne faut pas dériver, mais utiliser les fonctions usuelles.

C.a.d., réecrire ce qu'a écrit Ben314, avec les notations mathématiques.

[Pouletbraisé]

Ben 314 m'a bien expliqué pour la question B, c'est pour la C que je ne pige plus du tout ce qu'il faut faire