Fonction Trigo
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 19:48
par orangeverte » 21 Sep 2010, 19:48
Bonsoir,
Pouvez vous m'aider a résoudre cette fonction svp :
 = cos^2x.sin2x)
merci :we:
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 19:51
par Rebelle_ » 21 Sep 2010, 19:51
Bonsoir =)
Que veux-tu dire par "résoudre cette fonction" ? Attention aux termes employés :)
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 19:53
par orangeverte » 21 Sep 2010, 19:53
je veux dire etudier :)
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 19:59
par Rebelle_ » 21 Sep 2010, 19:59
Ah, eh bien dis "étudier la fonction", sinon ce n'est pas clair :)
Pour l'ensemble de définition ça ne devrait pas être très dur : y a-t-il des valeurs interdites ?
Ensuite, tu peux peut-être remarquer que cette fonction est périodique et le montrer ? ;)
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 19:59
par orangeverte » 21 Sep 2010, 19:59
Son ensemble de def est bien [-1;1] ou IR?
Apres j'ai trouvé qu'elle était impaire.
Mais pour la dérivé j'ai plus de mal
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 20:01
par Rebelle_ » 21 Sep 2010, 20:01
Comment justifies-tu cet ensemble de définition ? Il faut toujours justifier :)
Elle est impaire ? Pourquoi ?
Pour la dérivée, te rappelles-tu de la formule de la dérivée d'un produit de fonctions ? :)
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 20:04
par orangeverte » 21 Sep 2010, 20:04
^^ '
Je ne pense pas qu'il y est de valeur interdite donc je pense que c'est IR,
Pour la parité deja elle est centré en 0 et f(-x) = -f(x) non ?
Le produit de dérivé je sais le faire mais après ca me donne un résultat bizarre
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 20:07
par Rebelle_ » 21 Sep 2010, 20:07
Le fait qu'elle soit "centrée" en 0 (en plus de ne pas signifier grand chose :/) ne prouve rien. En effet, elle est impaire car f(-x) = -f(x) pour tout x réel (l'ensemble de définition). Donc, la courbe de f admet l'origine du repère comme centre de symétrie.
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 20:09
par orangeverte » 21 Sep 2010, 20:09
Pour la derive je ne suis pas sur, j'ai dit que la derive de cos^2x est -sin^2x, c'est faux non ?
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 20:14
par Rebelle_ » 21 Sep 2010, 20:14
Hum il faut prendre ça dans l'ordre.
Peux-tu compléter ceci : Si u et v sont deux fonctions dérivables sur un même intervalle I alors la fonction produit uv est dérivable sur I et, pour tout x de I, on a (uv)'(x) = ...
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 20:15
par orangeverte » 21 Sep 2010, 20:15
(uv)'= u'v + uv'
ca ca va c'est pour la dérivé de
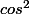
que je bug
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 20:23
par Rebelle_ » 21 Sep 2010, 20:23
Oh mais c'est très facile :)
cos²(x) est de la forme u²(x) où u est cos, et donc la dérivée est de la forme... (je crois que c'est dans le cours :P)
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 20:25
par orangeverte » 21 Sep 2010, 20:25
c'est 2cosx ?
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 20:26
par Rebelle_ » 21 Sep 2010, 20:26
La dérivée de u² c'est 2uu', et donc... ?
Allez, courage =)
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 20:30
par orangeverte » 21 Sep 2010, 20:30
Alors ca doit etre 2cosx.(-sinx) non ?
la derivee f^2 je l'ai pas vu en cours
merci :)
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 20:33
par Rebelle_ » 21 Sep 2010, 20:33
Cette dérivée découle de la formule de la dérivée de deux fonctions sauf qu'ici les deux fonctions en question sont égales ;)
Il doit y avoir un problème avec ta dérivée, je trouve f'(x) = 2cos²(x)*cos(2x) - 2sin(x)*sin(2x)*cos(x), sauf erreur.
Tu peux me montrer tes étapes si tu veux :)
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 20:39
par orangeverte » 21 Sep 2010, 20:39
je regarde 2s :)
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 20:42
par orangeverte » 21 Sep 2010, 20:42
Mise a jour ;
j'ai :
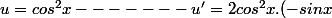 --------<br />v = sin2x ------- v'= cos2x)
' = -sinx.2cos^2x.sin2x+cos^2x . cos2x)
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 21 Sep 2010, 20:51
par Rebelle_ » 21 Sep 2010, 20:51
Alors attention, regardons :
(sin2x)' = cos2x*(2x)', soit...
-
orangeverte
- Membre Naturel
- Messages: 29
- Enregistré le: 14 Sep 2010, 17:51
-
 par orangeverte » 21 Sep 2010, 20:54
par orangeverte » 21 Sep 2010, 20:54
je comprend pas bien le cos2x.(2x)' dsl tu peux m'eclaircir stp ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités