Fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
bader50
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Mai 2009, 15:18
-
 par bader50 » 22 Mai 2009, 15:40
par bader50 » 22 Mai 2009, 15:40
bonjour je dois développer A(x)=(x-4)²(2+x) et B(x)=(2-x)[(x-2)²-12]
voila ce que j'ai trouver
A(x)=(x-4)²(2+x)
=(x²-8x+16)(2+x)
=2x²+x^3-16x-8x²+32+16x ( x^3 = x au cube )
=-6x²+x^3+32
B(x)= (2-x)[(x-2)²-12]
=(2-x)[x²-4x+4-12]
=(2-x)(x²-4x-8)
=2x²-8x-16-x^3+4x²+8x
=6x²-16-x^3
voila pour le développement j'espère que c'est juste merci de corriger mes erreur, mais il faut aussi factoriser B(x) mais je trouve pas comment faire merci de m'éclairer :help:
-
maturin
- Membre Irrationnel
- Messages: 1193
- Enregistré le: 09 Nov 2006, 16:28
-
 par maturin » 22 Mai 2009, 15:49
par maturin » 22 Mai 2009, 15:49
c'es tout bon pour les développement.
Pour factoriser B, part de la forme non développée de l'énoncé tu as déjà (2-x) en facteur.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 15:51
par Ericovitchi » 22 Mai 2009, 15:51
pour factoriser B(x)=(2-x)[(x-2)²-12] il faut traiter [(x-2)²-12] comme un

-
luffy37
- Membre Naturel
- Messages: 54
- Enregistré le: 13 Avr 2008, 23:23
-
 par luffy37 » 22 Mai 2009, 15:55
par luffy37 » 22 Mai 2009, 15:55
Ton A et B sont bon.
Pour B je pense que l'on te demande de factoriser en mettant sous la forme de deux polynomes.
Tu auras donc quelque chose comme:
(ax-b)*(ax²+cx+d)
A toi de trouver a,b,c,d

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 15:59
par Ericovitchi » 22 Mai 2009, 15:59
ben non, si c'était 2 polynômes il aurait déjà la réponse (2-x)(x²-4x-8)
il faut trouver 3 polynômes et pour ça il faut traiter [(x-2)²-12] comme un
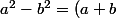(a-b))
-
bader50
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Mai 2009, 15:18
-
 par bader50 » 22 Mai 2009, 16:11
par bader50 » 22 Mai 2009, 16:11
si je fait:
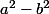
sa donne:
B(x)=(2-x)[(x-2)²-12]
=(2-x) [(x-2)-6] [(x-2)+6]
et la je crois que c'est résolue
et avec (ax-b)*(ax²+cx+d) je c'est pas comment faire dans l'exercice on me dit "Factoriser B(x)" c'est tout

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 16:34
par Ericovitchi » 22 Mai 2009, 16:34
ha bon ! la racine carré de 12 c'est 6 ? :cry:
-
bader50
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Mai 2009, 15:18
-
 par bader50 » 22 Mai 2009, 16:38
par bader50 » 22 Mai 2009, 16:38
j'avoue que je suis null :marteau: :stupid_in
sa fera donc B(x)= (2-x) [(x-2)-3.5] [(x-2)+3.5]
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 22 Mai 2009, 16:40
par Cheche » 22 Mai 2009, 16:40
Salut Bader50,
J'ai une petite astuce si tu veux rapidement savoir si tes résultats sont bons.
Tu essayes avec des valeurs simples de x.
exemple 1 : A(x)=(x-4)²(2+x) = -6x²+x^3+32
Si je pose : x = 0. Je trouve 32 = 32.
Si je pose : x = 1. Je trouve (-3)²*3= 27 = -6 +1 +32 = 27.
exemple 2 : B(x) = (2-x)[(x-2)²-12] =6x²-16-x^3
Si je pose : x = 0. Je trouve 2* (4-12) = -16 = -16
Si je pose : x = 1. Je trouve 1* (1-12) = -11 = 6 - 16 - 1 = -11
Il semblerait donc que tu aies bon. De plus cette méthode te permet de travailler ton calcul mental, une pas si mauvaise chose.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 16:41
par Ericovitchi » 22 Mai 2009, 16:41
ha bon ! la racine carré de 12 c'est 3.5 ? :cry:
-
bader50
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Mai 2009, 15:18
-
 par bader50 » 22 Mai 2009, 16:50
par bader50 » 22 Mai 2009, 16:50
j'ai arrondie le résultat mais j'ai compris ce tu veut dire
voila cette fois ci sa sera bon :
=(2-x)[(x-2)-sqrt{12}][(x-2)+sqrt{12}])
merci cheche pour la méthode

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 16:53
par Ericovitchi » 22 Mai 2009, 16:53
si tu te mets à arrondir les résultats dans les calculs algébriques, tu auras zéro.
et

-
bader50
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Mai 2009, 15:18
-
 par bader50 » 22 Mai 2009, 16:57
par bader50 » 22 Mai 2009, 16:57
c'est bon c'est sa le résultat ??

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 17:02
par Ericovitchi » 22 Mai 2009, 17:02
Oui. Tu peux juste enlever un peu des parenthèses mais c'est juste :
=(2-x)(x-2-2sqrt{3})(x-2+2sqrt{3}))
-
bader50
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Mai 2009, 15:18
-
 par bader50 » 22 Mai 2009, 17:25
par bader50 » 22 Mai 2009, 17:25
merci beaucoup pour votre aide sans vous je c'est pas ce que je vais faire
j'ai continuer l'exercice on m'a dit
A(x)=0
(x-4)²(x+2) = 0
<=> -6x²+x^3+32=0
<=> -6x²+x^3=-32
<=> x²+x^3=32/6
et la je suis bloquer

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 17:30
par Ericovitchi » 22 Mai 2009, 17:30
Pourquoi développes tu ? il est beaucoup plus facile de trouver quand A(x) = 0 sous la forme (x-4)²(x+2) = 0
pour que le produit soit nul il suffit que l'un des facteurs soit nul, donc il suffit de les annuler un par un et trouver les x qui correspondent.
-
bader50
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Mai 2009, 15:18
-
 par bader50 » 22 Mai 2009, 17:39
par bader50 » 22 Mai 2009, 17:39
est ce que c'est sa
(x-4)²= 0
})
² =0
x=4
x+2=0
x= -2
S(x) = {-2;4}

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 18:53
par Ericovitchi » 22 Mai 2009, 18:53
oui tout à fait
-
bader50
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Mai 2009, 15:18
-
 par bader50 » 22 Mai 2009, 19:02
par bader50 » 22 Mai 2009, 19:02
merci :we:
et la on me demande de démontrer que si x

[0;6] alors A(x)

0

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Mai 2009, 19:16
par Ericovitchi » 22 Mai 2009, 19:16
oui ? étudier le signe de (x-4)²(x+2), ça te pose problème ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 102 invités
