Fonction

[dodo555]

Bonjour je dois étudier la continuité d'une fonction en 0 mais je ne sais pas par où commencer.

La fonction f est définie sur R par f(x)= (e^2x - e^x) / x et f(0)= 1 .

MErci pour vos réponses

[Arnaud-29-31]

Bonjour,

Qu'est ce qu'une fonction continue pour toi ?

[Ericovitchi]

en regardant si la limite de f(x) quand x tends vers zéro est 1 ou pas

[dodo555]

en regardant si la limite de f(x) quand x tends vers zéro est 1 ou pas

Quand je fais la limite de f(x) quand x tends vers 0 je trouve 0.

Est ce normal?

[Arnaud-29-31]

Non ...
Comment t'y prends tu pour calculer cette limite ?

[dodo555]

Non ...
Comment t'y prends tu pour calculer cette limite ?

Bah je fais lim quand x tend vers 0 de e^2x - e^x / x

Cest la lim quand x tend vers 0 de e^2x = 1

moins la limite quand x tend vers 0 de e^x = 1

diviser par la limite quand x tend vers 0 de x = 0

donc 1-1/0 = 0

:s

[Arnaud-29-31]

Oulaaa ...

Donc si f tend vers 0 et g tend vers 0 alors f/g tend vers 0 ??

[dodo555]

Oulaaa ...

Donc si f tend vers 0 et g tend vers 0 alors f/g tend vers 0 ??

Non cest bon enfait j'ai trouvé il fallait facotrisé par e^x et aprés ca nous donné une limite du cours.

Maintenant comment faire pour répondre à cette question:

est elle continue sur R?

[Arnaud-29-31]

Eh bien tu sais que par propriété de l'exponentielle que f(x) est continue sur et sur .
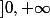Et le fait que montre la continuité en 0.

[dodo555]

Eh bien tu sais que par propriété de l'exponentielle que f(x) est continue sur et sur .
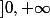Et le fait que montre la continuité en 0.

Et je conclue en disant qu'elle est continue sur R?

[Arnaud-29-31]

C'est quoi la définition d'une fonction continue sur R ?

[dodo555]

C'est quoi la définition d'une fonction continue sur R ?

On dit qu'une fonction f est continue sur R ou sur un intervalle ouvert I de si elle est continue en tout point de R ou de cet intervalle.

[dodo555]

On dit qu'une fonction f est continue sur R ou sur un intervalle ouvert I de si elle est continue en tout point de R ou de cet intervalle.

Pour linstant je peux pas affirmer qu'elle est continue sur R puisque j'ai démontré qu'elle était continue qu' en 0

[Arnaud-29-31]

Eh bien tu sais que par propriété de l'exponentielle que f(x) est continue sur et sur .
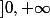Et le fait que montre la continuité en 0.

On montre d'abord la continuité "partout sauf en certains points" et ensuite on s'occupe des points qui posent problème.

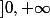La continuité sur et sur ne devrait pas posé de problème ...