Fonction reciproque racine cubique
5 messages
- Page 1 sur 1
Re: Fonction reciproque racine cubique
g se simplifie
=3x^2+4x=y)
soit
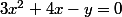
) et
et
)
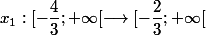
soit
Modifié en dernier par mathelot le 25 Nov 2018, 21:39, modifié 2 fois.
Re: Fonction reciproque racine cubique
soient f et g deux bijections réciproques.
on pose f(x)=a et f(y)=b ,i.e, x=g(a) et y=g(b)
on a l'égalité sur les taux de variation:
-f(y)}{x-y}=\dfrac{a-b}{g(a)-g(b)})
donc et
et 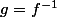 ont même sens de variation.
ont même sens de variation.
ainsi, pour en revenir à l'exercice:
La restriction de f est décroissante et bijective de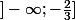 sur
sur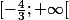
et admet pour réciproque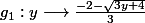
La restriction de f est croissante et bijective de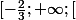 sur
sur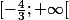
et admet pour réciproque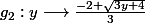
conclusion:
f admet à droite deux inverses g1 et g2:
})
on pose f(x)=a et f(y)=b ,i.e, x=g(a) et y=g(b)
on a l'égalité sur les taux de variation:
donc
ainsi, pour en revenir à l'exercice:
La restriction de f est décroissante et bijective de
et admet pour réciproque
La restriction de f est croissante et bijective de
et admet pour réciproque
conclusion:
f admet à droite deux inverses g1 et g2:
Re: Fonction reciproque racine cubique
Bonjour;
Je crois que la fonction est la fonction définie et continue sur
est la fonction définie et continue sur  par :
par : =\sqrt[3]{x^3+3x^2+3x}) .
.
On a :=\dfrac{(x+1)^2}{\sqrt[3]{x^3+3x^2+3x}^2}=\left (\dfrac{x+1}{\sqrt[3]{x^3+3x^2+3x}}\right )^2=\left (\dfrac{x+1}{\sqrt[3]{x(x^2+3x+3)}}\right )^2) .
.
Vu que le discriminant de l'expression :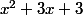 est strictement négatif , alors la fonction
est strictement négatif , alors la fonction  est dérivable sur
est dérivable sur 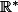
et s'annule pour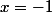 ; donc
; donc  est strictement positive sur
est strictement positive sur 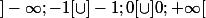 , donc
, donc  est strictement croissante sur
est strictement croissante sur  .
.
 est continue et strictement croissante sur
est continue et strictement croissante sur  , alors elle admet une fonction réciproque
, alors elle admet une fonction réciproque 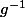 .
.
Pour trouver la fonction réciproque , il te suffit de remarquer que :
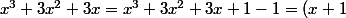^3 - 1) .
.
Bon courage pour la suite .
Je crois que la fonction
On a :
Vu que le discriminant de l'expression :
et s'annule pour
Pour trouver la fonction réciproque , il te suffit de remarquer que :
Bon courage pour la suite .
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
