La fonction racine carrée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sovietos
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Avr 2007, 16:30
-
 par Sovietos » 09 Mai 2007, 17:37
par Sovietos » 09 Mai 2007, 17:37
Bonjour Bonjour :we:
Une petite question de passage, assez simple :La fonction racine carrée est la fonction f définie sur [0 ; + infini[ par f(x) = R(x)
Etudions le sens de variation de f sur [0 ; + infini[.
Soitent a et b deux réels tels que 0<=a < b .
Démontrer que R(b) - R(a) = b-a / R(b) + R(a) .
Que peut-on en déduire pour le signe de R(b) - R(a) ?Je ne sait pas comment m'y prendre, si quelqu'un pouvait me guider :stupid_in Merci Beaucoup  Note : R(...) = racine carrée de ...
Note : R(...) = racine carrée de ...
-
Jess19
- Membre Irrationnel
- Messages: 1882
- Enregistré le: 02 Aoû 2006, 17:11
-
 par Jess19 » 09 Mai 2007, 17:39
par Jess19 » 09 Mai 2007, 17:39
c'est toi qui as fait le début de la démo ou ton prof ?
-
Sovietos
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Avr 2007, 16:30
-
 par Sovietos » 09 Mai 2007, 17:42
par Sovietos » 09 Mai 2007, 17:42
Tout ce qui est en bleu, ça vient de mon livre : l'exo en lui-même.
-
Jess19
- Membre Irrationnel
- Messages: 1882
- Enregistré le: 02 Aoû 2006, 17:11
-
 par Jess19 » 09 Mai 2007, 17:45
par Jess19 » 09 Mai 2007, 17:45
ok...
t'es d'accord que b-a < 0
et que racine de a + racine de b >0 car a et b sont positifs
donc racine de a - racine de b <0 d'où racine de a < racine de b
la fonction racine carrée est dc croissante sur R+
voilà je t'ai tout fait je peux pas mieux faire !
bonne continuation...
-
Sovietos
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Avr 2007, 16:30
-
 par Sovietos » 09 Mai 2007, 18:30
par Sovietos » 09 Mai 2007, 18:30
Jess19 a écrit:ok...
t'es d'accord que b-a 0 car a et b sont positifs
donc racine de a - racine de b <0 d'où racine de a < racine de b
la fonction racine carrée est dc croissante sur R+
voilà je t'ai tout fait je peux pas mieux faire !
bonne continuation...
Hm, merci, mais c'était déjà dis, ou sous-entendu dans l'énoncé...
Si je pouvais savoir comment démontrer le premier calcul, je pourrai entamer l'exercice plus... rapidement :space:
-
Jess19
- Membre Irrationnel
- Messages: 1882
- Enregistré le: 02 Aoû 2006, 17:11
-
 par Jess19 » 09 Mai 2007, 18:35
par Jess19 » 09 Mai 2007, 18:35
quel premier calcul ?
-
Sovietos
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Avr 2007, 16:30
-
 par Sovietos » 09 Mai 2007, 18:36
par Sovietos » 09 Mai 2007, 18:36
L'équation : R(b) - R(a) = b-a / R(b) + R(a)
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 09 Mai 2007, 18:39
par Clembou » 09 Mai 2007, 18:39
Sovietos a écrit:Bonjour Bonjour :we:
Une petite question de passage, assez simple :La fonction racine carrée est la fonction f définie sur [0 ; + infini[ par f(x) = R(x)
Etudions le sens de variation de f sur [0 ; + infini[.
Soitent a et b deux réels tels que 0<=a < b .
Démontrer que R(b) - R(a) = b-a / R(b) + R(a) .
Que peut-on en déduire pour le signe de R(b) - R(a) ?Je ne sait pas comment m'y prendre, si quelqu'un pouvait me guider :stupid_in Merci Beaucoup  Note : R(...) = racine carrée de ...
Note : R(...) = racine carrée de ...
Qu'est ce que donne le développement de
(\sqrt{a}+\sqrt{b}))
-
Sovietos
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Avr 2007, 16:30
-
 par Sovietos » 09 Mai 2007, 18:48
par Sovietos » 09 Mai 2007, 18:48
Euh, a - b ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 09 Mai 2007, 18:50
par Clembou » 09 Mai 2007, 18:50
Sovietos a écrit:Euh, a - b ?
Ah non excuses moi

c'est dans l'autre sens : tu pars de :
(\sqrt{b}+\sqrt{a}) = b-a)
et ensuite tu divises par
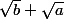
dans les deux termes de l'égalite...
-
Sovietos
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Avr 2007, 16:30
-
 par Sovietos » 09 Mai 2007, 18:57
par Sovietos » 09 Mai 2007, 18:57
Clembou a écrit:Ah non excuses moi

c'est dans l'autre sens : tu pars de :
(\sqrt{b}+\sqrt{a}) = b-a)
et ensuite tu divises par
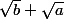
dans les deux termes de l'égalite...
Ce qui donne b - a / R(b) + R(a) = b*R(b) - a*R(a) / b + a ... je sais pas si je vais dans le bon sens là :hum:
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 09 Mai 2007, 19:00
par Clembou » 09 Mai 2007, 19:00
Sovietos a écrit:Ce qui donne b - a / R(b) + R(a) = b*R(b) - a*R(a) / b + a ... je sais pas si je vais dans le bon sens là :hum:
Ah non !!!
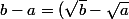(\sqrt{b}+\sqrt{a}))

-
Sovietos
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Avr 2007, 16:30
-
 par Sovietos » 09 Mai 2007, 19:06
par Sovietos » 09 Mai 2007, 19:06
Clembou a écrit:Ah non !!!
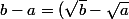(\sqrt{b}+\sqrt{a}))

Il faut donc trouver un lien entre ces deux calculs ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 09 Mai 2007, 19:09
par Clembou » 09 Mai 2007, 19:09
Sovietos a écrit:Il faut donc trouver un lien entre ces deux calculs ?
Ba non en fait...
La première égalité, on la trouve en faisant un développement puis la deuxième s'obtient en divisant par
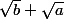
les deux termes de l'équation...
-
Sovietos
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Avr 2007, 16:30
-
 par Sovietos » 09 Mai 2007, 19:12
par Sovietos » 09 Mai 2007, 19:12
Clembou a écrit:Ba non en fait...
La première égalité, on la trouve en faisant un développement puis la deuxième s'obtient en divisant par
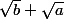
les deux termes de l'équation...
On a donc démontrer le calcul ? :stupid_in
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 281 invités
