Fonction pathologique continue et nulle part dérivable.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Aoû 2010, 15:58
par Nightmare » 26 Aoû 2010, 15:58
Il faut voir que (un) étant majorée en valeur absolue, sa borne sup est elle même majorée par le dit majorant.
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 26 Aoû 2010, 16:19
par GeorgeB » 26 Aoû 2010, 16:19
Merci de cette réponse mais malheureusement je ne vois pas ce que ça change, on s'intéresse à (Sn(x))n et Rn(x) , je pense que ton indication est pour la III-2 ,
-
Anonyme
 par Anonyme » 26 Aoû 2010, 16:23
par Anonyme » 26 Aoû 2010, 16:23
Je continue:
III-1
Soit

la limite de
)
(elle existe d'apres la question precedente).
On a
= S(x)-S_n(x))
A l'infini
= l-l =0)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 26 Aoû 2010, 16:26
par benekire2 » 26 Aoû 2010, 16:26
Ah, d'accord... je ne voyais pas ça comme ça, c'est aussi bête :briques:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 26 Aoû 2010, 16:27
par benekire2 » 26 Aoû 2010, 16:27
J'attaque ça ce soir, quand j'aurais réussi intégrer une certaine fonction :zen:
-
Anonyme
 par Anonyme » 26 Aoû 2010, 16:36
par Anonyme » 26 Aoû 2010, 16:36
Nightmare pour la III-2 c'est pas la meme demo que pour II-3 ?
-
Anonyme
 par Anonyme » 26 Aoû 2010, 16:47
par Anonyme » 26 Aoû 2010, 16:47
Pour la III-2 voila ce que j'ai trouver:
||_{\infty}= \frac{1}{2^{2k+1})
et donc a partir de la je trouve que la fonction est convergente pour tout entier N ( <n bien sur) en particulier si
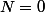
on trouve
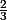
d'apres un calcul precedent.
A moins que je n'ai pas bien compris la question ..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Aoû 2010, 17:01
par Nightmare » 26 Aoû 2010, 17:01
Ca me va. Le but est simplement d'arriver à la convergence uniforme de S(n).
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 26 Aoû 2010, 17:02
par benekire2 » 26 Aoû 2010, 17:02
Qmath a écrit:Pour la III-2 voila ce que j'ai trouver:
||_{\infty}= \frac{1}{2^{2k+1})
et donc a partir de la je trouve que la fonction est convergente pour tout entier N ( <n bien sur) en particulier si
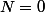
on trouve
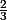
d'apres un calcul precedent.
A moins que je n'ai pas bien compris la question ..
Je crois que c'est faux, enfin c'est l'idée mais on peut juste dire que le sup des u_n est inférieur ou égal au majorant que tu as, mais on peut pas faire mieux, cela dit ça suffit a majorer la somme.
-
Anonyme
 par Anonyme » 26 Aoû 2010, 17:09
par Anonyme » 26 Aoû 2010, 17:09
benekire2 a écrit:Je crois que c'est faux, enfin c'est l'idée mais on peut juste dire que le sup des u_n est inférieur ou égal au majorant que tu as, mais on peut pas faire mieux, cela dit ça suffit a majorer la somme.
Je ne pense pas qu'il peut etre inferieur il est toujours egal a ce majorant.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Aoû 2010, 17:10
par Nightmare » 26 Aoû 2010, 17:10
1/(2^(2k+1)) étant atteint, ce qu'a écrit Qmath est bien juste. Néanmoins, comme tu le signales, autant se contenter d'un
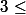
.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 26 Aoû 2010, 17:37
par benekire2 » 26 Aoû 2010, 17:37
Autant pour moi alors ^^ :zen:
-
Anonyme
 par Anonyme » 26 Aoû 2010, 18:39
par Anonyme » 26 Aoû 2010, 18:39
Qmath a écrit:Pour la III-2 voila ce que j'ai trouver:
||_{\infty}= \frac{1}{2^{2k+1})
et donc a partir de la je trouve que la fonction est convergente pour tout entier N ( <n bien sur) en particulier si
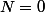
on trouve
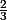
d'apres un calcul precedent.
A moins que je n'ai pas bien compris la question ..
Comme c'est vrai pour tout N j'en deduis que
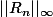
tend vers 0. C'est direct non ?
Je vais voir la definition de convergence unfiorme ...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Aoû 2010, 18:43
par Nightmare » 26 Aoû 2010, 18:43
Si tu te poses la question de savoir si c'est direct, c'est que ce n'est pas direct :lol3:
Pour la définition de la convergence uniforme, je l'ai (presque) donnée.
-
Anonyme
 par Anonyme » 26 Aoû 2010, 18:57
par Anonyme » 26 Aoû 2010, 18:57
Nightmare a écrit:Si tu te poses la question de savoir si c'est direct, c'est que ce n'est pas direct :lol3:
Pour la définition de la convergence uniforme, je l'ai (presque) donnée.
C'est plus une question rhetorique qu'une vraie question :lol3:
Oui j'ai vu la definition .. mais pourquoi le "(presque)" ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Aoû 2010, 19:41
par Nightmare » 26 Aoû 2010, 19:41
Je l'ai donnée pour une suite de fonction uniformément convergent vers 0, pour une limite quelconque, il suffit bien sûr de remplacer 0 par la fonction.
-
Anonyme
 par Anonyme » 26 Aoû 2010, 20:05
par Anonyme » 26 Aoû 2010, 20:05
Alors maintenant il s'agit de demontrer que
)
converge uniformement vers 0.
Pour n fixee on a:
 \leq ||R_n(x)||_{\infty})
==>
Or
||_{\infty}= \frac{4}{3} \time \frac{1}{2^{2n+3}}=\frac{1}{3\time2^{2n+1}})
Donc pour

fixee on peut trouver un entier

tel que
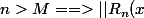||_{\infty} M, \forall x , R_n(x) \leq ||R_n(x)||_{\infty} M, \forall x , R_n(x) \leq ||R_n(x)||_{\infty} <\epsilon)
NB :J'ai pas mis des valeurs absolu car
)
est postive
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Aoû 2010, 20:25
par Nightmare » 26 Aoû 2010, 20:25
Correct une nouvelle fois !
-
Anonyme
 par Anonyme » 26 Aoû 2010, 20:39
par Anonyme » 26 Aoû 2010, 20:39
J'ai une question un peu hors sujet par rapport au TD.
Si une suite
)
tel que
||_{\infty} ---> l)
. Est ce que
>0)
est une condition necessaire a la convergence uniforme de
))
?
Ou bien c'est juste une condition suffisante ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 27 Aoû 2010, 11:31
par Nightmare » 27 Aoû 2010, 11:31
Salut,
Une suite de fonction peut converger uniformément vers sa limite en étant de tout signe !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
on trouve
d'apres un calcul precedent.
on trouve
d'apres un calcul precedent.
