Fonction (Niveau terminale STG)

[dewey]

Bonjour, je vien cherché de l'aide pour un exercice qui pourrait vous parraitent simple pour vous mais compliqué pour moi. :hein:

Soit la fonction f défiie sur [o;7] par f(x)= x(au cube)/3-3x(au carré)+5x+10

1- Calculer la dérivée de f sur [0;7]

2- Vérifier en développant eten détaillan les calculs que: pour tout réel x de [0;7] f'(x)=(x-1)(x-5)

3- En déduire le signe de f'(x) sur [o;7] puis les variations de f.

4- Dresser le tableau des vairations de f

[fonfon]

salut, as-tu réussi au moins à calculer la dérivée?

[dewey]

salut, as-tu réussi au moins à calculer la dérivée?

J'hésite entre f'=3x(au carré) -6x+ 5 et f'= 3x(au carré)/3-6x+5

[fonfon]

re,

ta fonction c'est donc je pencherais pour f'(x)= 3x(au carré)/3-6x+5 que tu peux ecrire

[dewey]

Et pour les autre question tu pourrait pas m'aidé?

[fonfon]

pour la 2) tu as du voir le dicriminant je pense ?

[dewey]

pour la 2) tu as du voir le dicriminant je pense ?

Eux ma classe oui mais moi non, j'ai du loupé des cour suite a des probleme familiale et j'ai pas eu le temps de tout rattrapé :'-(

[fonfon]

un rappel:

un polynôme du secon degré est une expression de la forme ax²+bx+c (a,b,c réels, a#0)

pour factoriser ce polynome on va chercher les racines du polynôme

on pose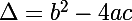

si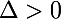 le polynôme a deux racines distinctes : 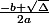ou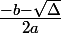

si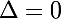 une racine double

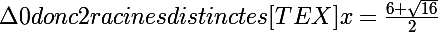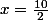si ou
ou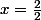
x=5 ou x=1

donc
f'(x)=x²-6x+5 f'(x)=(x-1)(x-5)


ensuite

3) tu te sers de f'(x)=(x-1)(x-5) tu fais un tableau de signe ds l'intervalle [0,7] ça te donnera le signe de f' et donc les variations de f

[dewey]

Et pour le 4), j'utilise cette fonction là: (x)= x(au cube)/3-3x(au carré)+5x+10?

[fonfon]

non, tu utilises la 3) apres avoir trouvé le signe de la dérivée sur [0,7] tu as les variations de ta fonction

normalement , ta fonction est croissante sur [0,1] (car f'>0 sur [0,1]), decroissante sur [1,5] ( car f'<0 sur [1,5]) et croissante sur [5,7] (car f'>0 sur [5,7])

voilà

[dewey]

merci beaucoup surtout pour le petit 2 qui est bien expliqué ^^