Fonction,Injection,Surjection 1ère S

[Kiritsugu]

Bonjour vous pouvez m'aider sur cet exercice j'ai un contrôle demain et
Il y a plusieurs exercices que j'aimerais pouvoir faire comme celui là:
Soit la fonction g:

1-Démontrer que g est injective.
2-Démontrer que g n'est pas surjective.

[chan79]

Bonjour vous pouvez m'aider sur cet exercice j'ai un contrôle demain et
Il y a plusieurs exercices que j'aimerais pouvoir faire comme celui là:
Soit la fonction g:

1-Démontrer que g est injective.
2-Démontrer que g n'est pas surjective.

salut
g(1,2)=g(1,3)

ou alors corrige le texte

[Kiritsugu]

Désolé mais j'ai l'impression que j'ai bel et bien recopié le texte.
Et merci pour ton idée je l'avait aussi remarquer que le y ne servait a rien .

[Kiritsugu]

Comment démontrer que g est injective ?

[mathelot]

Chan a prouvé que f n'est pas injective. Elle n'est pas surjective non plus:

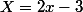
Si et



(**)
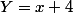
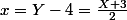
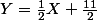
l'image de par f est la droite d'équation (**)

[Kiritsugu]

S'il te plait je ne voit pas du tout qu'elle est l'équation de la droite .