Bonjour
Quelqu'un pourrait-il m'expliquer ce que l'on entend par 'fonction implicite', ou me diriger vers un url qui explique ce dont il s'agit ?
Je voudrait savoir:
- Ce que c'est
- Quels sont les avantages de ce type de fonction
- Le cadre dans lequel ce type de fonction est utilisé
- Peut être quleques exemples ...
Merci d'avance
Vincent
Fonction implicite
3 messages
- Page 1 sur 1
Bonjour,
On se place dans un espace euclidien de dimension n.
Les courbes sont des ensembles de points.
Dès qu'un repère a été choisi, les points ont n coordonnées.
Dès lors, la courbe induit une relation entre les différentes coordonnées
d'un point (générique) de cette courbe.
On dira que (x,y,z,t) sont en relation si le point M(x,y,z,t)
appartient à la courbe considérée.
La courbe est décrite par une équation (une équation est une formule close
où apparaissent les n quantités variables)
de la forme F(x,y,z,t)=0 (**)
par exemple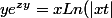+arctan(zt))
Il se peut, essentiellement à cause de la géométrie de la courbe,
que (**)
équivaut au fait que certaines coordonnées (par exemple x,z) soient déterminées de façon univoque, quand les autres coordonnées
(y,t) sont connues.
Dès lors , la flèche \rightarrow (x,z)) est à la fois une fonction et un paramètrage local de la courbe.
est à la fois une fonction et un paramètrage local de la courbe.
Ensuite, si la courbe est douce ("smooth"), la fonction F
k fois continuement différentiable, alors le paramétrage local
récupère les propriétés de différentiabilité de F.
Le théorème des fonctions implicites a énormément
d'applications:
- il permet de paramétrer localement les surfaces (les variétés)
et d'offrir ce que l'on appelle des coordonnées locales et des cartes
- du point de vue ensembliste, il permet d'établir des
bijections (exemple: le cercle est localement (rac de cercle) en correspondance avec un segment de droite)
-il donne des théorèmes d'existence de solutions d'équations différentielles
son gros défaut est d'être en théorème local. Le plus souvent,
le domaine de définition de la fonction implicite est un petit voisinage
La fonction implicite obtenue entre certaines coordonnées
obtenue entre certaines coordonnées
qui participent à une équation F(x,y,z,t) est obtenue , en pratique,via
par un développement limité, style Taylor-Young,
avec des formules utilisant les dérivées partielles successives de F.
Exemple de base:
le cercle a pour équation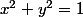
Localement, cette équation fait que x est fonction de y ou y est fonction de x.
si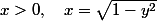
si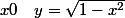
si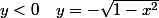
Autre exemple:
une équation algébrique de degré n
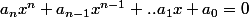
définit chaque solution comme fonction
comme fonction
implicite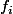 des coefficients
des coefficients 
ce qui permet de distinguer ces différentes fonctions implicites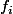
est le petit voisinage de choisi comme espace d'arrivée de la fonction implicite.
choisi comme espace d'arrivée de la fonction implicite.
Le fait pour la fonction d'être "implicite" signifie
- son existence est "locale"
- une formule close n'existe pas toujours et on doit se contenter de DL
On se place dans un espace euclidien de dimension n.
Les courbes sont des ensembles de points.
Dès qu'un repère a été choisi, les points ont n coordonnées.
Dès lors, la courbe induit une relation entre les différentes coordonnées
d'un point (générique) de cette courbe.
On dira que (x,y,z,t) sont en relation si le point M(x,y,z,t)
appartient à la courbe considérée.
La courbe est décrite par une équation (une équation est une formule close
où apparaissent les n quantités variables)
de la forme F(x,y,z,t)=0 (**)
par exemple
Il se peut, essentiellement à cause de la géométrie de la courbe,
que (**)
équivaut au fait que certaines coordonnées (par exemple x,z) soient déterminées de façon univoque, quand les autres coordonnées
(y,t) sont connues.
Dès lors , la flèche
Ensuite, si la courbe est douce ("smooth"), la fonction F
k fois continuement différentiable, alors le paramétrage local
récupère les propriétés de différentiabilité de F.
Le théorème des fonctions implicites a énormément
d'applications:
- il permet de paramétrer localement les surfaces (les variétés)
et d'offrir ce que l'on appelle des coordonnées locales et des cartes
- du point de vue ensembliste, il permet d'établir des
bijections (exemple: le cercle est localement (rac de cercle) en correspondance avec un segment de droite)
-il donne des théorèmes d'existence de solutions d'équations différentielles
son gros défaut est d'être en théorème local. Le plus souvent,
le domaine de définition de la fonction implicite est un petit voisinage
La fonction implicite
qui participent à une équation F(x,y,z,t) est obtenue , en pratique,via
par un développement limité, style Taylor-Young,
avec des formules utilisant les dérivées partielles successives de F.
Exemple de base:
le cercle a pour équation
Localement, cette équation fait que x est fonction de y ou y est fonction de x.
si
si
si
Autre exemple:
une équation algébrique de degré n
définit chaque solution
implicite
ce qui permet de distinguer ces différentes fonctions implicites
est le petit voisinage de
Le fait pour la fonction d'être "implicite" signifie
- son existence est "locale"
- une formule close n'existe pas toujours et on doit se contenter de DL
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
