Fonction exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 18:12
par Cher93 » 15 Déc 2018, 18:12
Bonjour tout le monde j’ai besoin de votre aide pour l’exercice suivant et merci d’avance:
Soit la fonction definie sur [0;+l’infin[ par:
f(x)=
 -1 }{\sqrt{x}})
et f(0)=0
1. Determiner la limite en + l’infini
2. Montrer que lim(t—>0)
 -1 }{t})
=-1 et en deduire que f est continue en 0.
3.Etudier la derivabilité de f en 0.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 18:22
par Carpate » 15 Déc 2018, 18:22
Qu'as-tu fait ?
1) Il n'y a pas d'indétermination
Quand

,

Quand
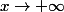
,

Modifié en dernier par
Carpate le 15 Déc 2018, 18:23, modifié 1 fois.
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 18:23
par Cher93 » 15 Déc 2018, 18:23
Oui +l’inf
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 18:23
par Cher93 » 15 Déc 2018, 18:23
Je bloque surtout dans les deux autres!!
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 18:25
par Carpate » 15 Déc 2018, 18:25
Oui +l’inf
Ca veut dire quoi ? Tu ne peux pas prendre la peine de t'exprimer clairement ?
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 18:41
par Cher93 » 15 Déc 2018, 18:41
La lim de f(x) =- l’inf
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 18:42
par Carpate » 15 Déc 2018, 18:42
Non ...


-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 18:54
par Cher93 » 15 Déc 2018, 18:54
D’accord! C’ est juste pour que cela soit un petit peu plus rapide! (Sachant que c’est une question deja que j’ai deja faite!) .
Pour la deuxieme question je trouve que c’est egal à =-1 , mais je ne vois pas comment en deduire la continuité de f en 0!
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 19:04
par Carpate » 15 Déc 2018, 19:04
C’ est juste pour que cela soit un petit peu plus rapide! (Sachant que c’est une question deja que j’ai deja faite!) .
C'était peut-être plus rapide mais ton résultat était faux.
Si
 = \frac{e^{-x}-1}{x})
,
 = \frac{g(x)}{\sqrt{x}})
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 19:23
par Cher93 » 15 Déc 2018, 19:23
Je ne comprends pas !
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 19:36
par Cher93 » 15 Déc 2018, 19:36
C’est pas g(x) =f(x)/ racine de x ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 19:38
par Carpate » 15 Déc 2018, 19:38
Oui !
Et j'ai envoyé le message précédent par erreur en message privé
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 19:59
par Carpate » 15 Déc 2018, 19:59
Donc je corrige
=\sqrt{x}.g(x))
Mais il me semble qu'on n'a pas besoin de cela pour monter que f est continue en 0
puisque
=0)
et
 =0)
donc
 = f(0))
donc f continue en 0
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 20:03
par Cher93 » 15 Déc 2018, 20:03
Comment demontrer que c’est egal à 0 en 0.
Avez vous utilisé l’expression f(c)=racine de x .g(x) Pas vrai?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 20:06
par Carpate » 15 Déc 2018, 20:06
Soit la fonction definie sur [0;+l’infini[ par:
=\frac{e^{-x}-1}{\sqrt{x}})
et
f(0)=0
C'est pas moi qui l'ai décidé mais c'est l'auteur de l'énoncé !
Ca s'appelle un prolongement par continuité .
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 20:23
par Cher93 » 15 Déc 2018, 20:23
Je parle de la limite*
Lim (x—>0) f(x)=0?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 21:20
par Carpate » 15 Déc 2018, 21:20
En 0, g(x) tend vers -1 donc
=\sqrt{x}. g(x))
tend vers (-1) * 0
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 15 Déc 2018, 21:56
par Cher93 » 15 Déc 2018, 21:56
Et pour la derivabilité ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 16 Déc 2018, 09:14
par Carpate » 16 Déc 2018, 09:14
_{x=0}=\lim_{h\rightarrow0}\frac{f(0+h)-f(0)}{h}=\lim_{h\rightarrow0}\frac{f(h)}{h})
}{h}=\frac{g(h)\sqrt{h}}{h}=\frac{g(h)}{\sqrt{h}})
Quand x --> 0, g(h) --> -1 et
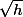
-- > 0 ,
}{\sqrt{h}} \rightarrow -\infty)
f non dérivable en 0 et tangente en 0 "verticale", orientée vers les ordonnées négatives
-
Cher93
- Membre Relatif
- Messages: 141
- Enregistré le: 17 Oct 2018, 12:32
-
 par Cher93 » 16 Déc 2018, 10:11
par Cher93 » 16 Déc 2018, 10:11
Merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités