Je ne sais pas quelle fonction tu as choisi d'étudier.
Si on prend la plus simple, c'est à dire
\!=\!x\exp(x))
de façon à avoir a
\!=\!\dfrac{1}{x}\ \Leftrightarrow\ g(x)\!=\!1)
.
Alors
\!=\!(1+x)\exp(x))
est du signe de
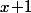
donc facile à déterminer.
La limites de

en -oo est 0 (cas connu) et celle en +oo est +oo (évident)
Donc tu trace le tableau de variation de g sans soucis et ça te permet de déterminer le nombre de solutions de l'équation
\!=\!1)
.
Sinon, quelque soit la fonction que tu as choisi d'étudier, si besoin (pour étudier le signe de la dérivée), tu peut fortement restreindre le domaine d'étude via quelque mini remarques qui sont évidentes en regardant le dessin qu'on a fait avec les courbes des deux fonctions :
- Si
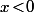
on ne risque pas d'avoir
\!=\!\dfrac{1}{x})
vu que
\!>\!0)
alors que

.
- Si

alors
\!\geq\!\exp(1)\!>\!1)
alors que

donc on ne risque de nouveau pas d'avoir
\!=\!\dfrac{1}{x})
.
Donc il suffit de regarder ce qu'il se passe pour

entre 0 et 1.
 n peut se ramener au cadre d'application de corollaire du TVI
n peut se ramener au cadre d'application de corollaire du TVI