Fonction dérivées Term. ES

[dodie94]

salut a tous moi c'est elodie jsuis en terminale ES et au cas ou j'aimerais aussi de l'aide sur le dernier exercices de mon dm merci psk si je comprend pas jsuis vraiment dans le caca XD

Exercice3
Le coût total de fabrication d’un produit est donnée par C(q)=(q^3/3)-(6q^2)+40q pour q E [0 ;12] où q représente le nombre de milliers d’unités fabriquées et C(q) le coût de fabrication en centaines d’euros.
1) On rappelle que le coût unitaire moyen est donné par CM(q)=C(q)/q pour tout q > 0.
a) Exprimer en fonction de q le coût unitaire moyen.
b) Calculer le nombre q0 d’unités à fabriquer pour que le coût moyen soit minimal.
2) On appelle coût marginal la dépense occasionnée par la production d’un objet supplémentaire. On modélise ce coût marginal par Cm(q) = C’(q) où C;) est la dérivée de C.
a) Exprimer en fonction de q le coût marginal.
b) Vérifier que pour q0, le coût marginal est égal au coût moyen.
3) On suppose que l’entreprise vend toute sa production. Pour q E]0 ; 12] le bénéfice en
centaines d’euros, pour la production de q milliers d’unités est B(q) = (-q^-3/3) + (2q^2) +21q
a) Calculer le nombre d’unités à produire pour que l’entreprise soit rentable.
b) Déterminer le nombre d’unités à fabriquer pour obtenir le bénéfice maximum. Que vaut ce bénéfice maximal ?

[Anonyme]

@dodie94

Peux tu au moins répondre à la question 1a)

Explications supplémentaires

On sait que C(q)=(q^3/3)-(6q^2)+40q

et on demande de calculer C(q)/q
pour obtenir ce qui est appelé le coût unitaire moyen

[dodie94]

@dodie94

Peux tu au moins répondre à la question 1a)

Explications supplémentaires

On sait que C(q)=(q^3/3)-(6q^2)+40q

et on demande de calculer C(q)/q
pour obtenir ce qui est appelé le coût unitaire moyen

euhh c'est que est ce que je dois calculer la dérivée nan mais je comprend vraiment pas et j'ai un ami qui était en sti et qui a u 17 a son bac de maths qui n'a pas compris alrs c' est ke sa doit vraiment pas être facile ...

[Anonyme]

1) On rappelle que le coût unitaire moyen est donné par CM(q)=C(q)/q pour tout q > 0

Que veut dire pour toi ce rappel ?

[dodie94]

Que veut dire pour toi ce rappel ?

ba jpense qu'il faut calculer la dérivé ou je non je sais vraiment pas jcomprend pas la question et puis comment on calcul sa C(q)/q

[Anonyme]

@dodie94

C(q)/q = [ (q^3/3)-(6q^2)+40q ] /q

Et tu peux simplifier cette fraction ( qui représente CM(q) qui est la question 1a) )

[dodie94]

@dodie94

C(q)/q = [ (q^3/3)-(6q^2)+40q ] /q

Et tu peux simplifier cette fraction ( qui représente CM(q) qui est la question 1a) )

ptin et moi qui cherchait compliqué ... --'

[Anonyme]

@dodie94
Les maths : c'est FORCEMENT très compliquées si quand on lit l'énoncé d'un exercice on n'écrit rien sur une feuille de papier !

Lire un énoncé sans rien écrire : veut dire tout retenir dans son cerveau et faire cogiter à donf ses neurones...

Ce message ne veut pas dire que tu as une petite tête ou pas assez de neurones pour faire des maths :-)

Le but de ce message est pour : qu'au prochain exercice de maths , tu essaies d'appliquer cette méthode
1) lire attentivement l'énoncé
2) écrire sur une feuille ce que tu as compris de l'énoncé

A+

[dodie94]

@dodie94
Les maths : c'est FORCEMENT très compliquées si quand on lit l'énoncé d'un exercice on n'écrit rien sur une feuille de papier !

Lire un énoncé sans rien écrire : veut dire tout retenir dans son cerveau et faire cogiter à donf ses neurones...

Ce message ne veut pas dire que tu as une petite tête ou pas assez de neurones pour faire des maths

Le but de ce message est pour : qu'au prochain exercice de maths , tu essaies d'appliquer cette méthode
1) lire attentivement l'énoncé
2) écrire sur une feuille ce que tu as compris de l'énoncé

A+

ouai jsuis d'accord avec ce que tu dis tkt mais j'essaye de simplifier la fraction et perso jcomprend pas a par si la derivée intervient et que cela fasse [q^2-12q+40]/q

[Anonyme]

@dodie94

On a c(q)=(q^3/3)-(6q^2)+40q

1) calcul du coût unitaire moyen
CM(q)=C(q)/q = [ (q^3/3)-(6q^2)+40q ] / q = (q^2/3)-(6q)+40

2) calcul du coût marginal
Cm(q) = C’(q) = (u+v+w)'(q)

avec u(q)= q^3/3 et v(q)= -(6q^2) et w(q) = 40q

D'après des formules du cours on sait que
u'(q)= q^2
v'(q)=-12q
w'(q)=40
et que (u+v+w)'(q)=u'(q)+v'(q)+w'(q)

donc Cm(q) = C’(q) = q^2-12q+40

Essaie de continuer à travailler cet exo et n'hésite pas à poser d'autres questions


ps)
Dans cet exercice la variable des fonctions est
( au lieu généralement de )

Pour calculer des fonctions dérivées , on dérive par rapport à cette variable
( et cela revient à appliquer les formules du cours en remplaçant par )

[dodie94]

@dodie94

On a c(q)=(q^3/3)-(6q^2)+40q

1) calcul du coût unitaire moyen
CM(q)=C(q)/q = [ (q^3/3)-(6q^2)+40q ] / q = (q^2/3)-(6q)+40

2) calcul du coût marginal
Cm(q) = C’(q) = (u+v+w)'(q)

avec u(q)= q^3/3 et v(q)= -(6q^2) et w(q) = 40q

D'après des formules du cours on sait que
u'(q)= q^2
v'(q)=-12q
w'(q)=40
et que (u+v+w)'(q)=u'(q)+v'(q)+w'(q)

donc Cm(q) = C’(q) = q^2-12q+40

Essaie de continuer à travailler cet exo et n'hésite pas à poser d'autres questions


ps)
Dans cet exercice la variable des fonctions est
( au lieu généralement de )

Pour calculer des fonctions dérivées , on dérive par rapport à cette variable
( et cela revient à appliquer les formules du cours en remplaçant par )

est ce que pour la question 1) b. il faut remplacer q par 0 et donc cela donne: (0^2/3)-12*0+40=40
Ensuite la 2)a. comme tu me l'a expliqué ont doit dire la dérivée donc q^2-12q+40
2)b. Donc la si on refait pareil on remarque que 0^2-12*0+40=40 comme pour le coût moyen
3) après je n'est pas bien compris comment calculer le nombres d'unités pour que l'entreprise soit rentable peut tu me dire si j'ai juste aux questions précédentes et m'aider pour les suivantes?

[dodie94]

@dodie94

On a c(q)=(q^3/3)-(6q^2)+40q

1) calcul du coût unitaire moyen
CM(q)=C(q)/q = [ (q^3/3)-(6q^2)+40q ] / q = (q^2/3)-(6q)+40

2) calcul du coût marginal
Cm(q) = C’(q) = (u+v+w)'(q)

avec u(q)= q^3/3 et v(q)= -(6q^2) et w(q) = 40q

D'après des formules du cours on sait que
u'(q)= q^2
v'(q)=-12q
w'(q)=40
et que (u+v+w)'(q)=u'(q)+v'(q)+w'(q)

donc Cm(q) = C’(q) = q^2-12q+40

Essaie de continuer à travailler cet exo et n'hésite pas à poser d'autres questions


ps)
Dans cet exercice la variable des fonctions est
( au lieu généralement de )

Pour calculer des fonctions dérivées , on dérive par rapport à cette variable
( et cela revient à appliquer les formules du cours en remplaçant par )

Au faite je dois rendre ce dm jeudi et samedi qui vient j'ai un DST de maths sur le même type d'exercice...

[Anonyme]

Le coût total de fabrication d’un produit est donnée par C(q)=(q^3/3)-(6q^2)+40q pour q E [0 ;12] où q représente le nombre de milliers d’unités fabriquées et C(q) le coût de fabrication en centaines d’euros.
1) On rappelle que le coût unitaire moyen est donné par CM(q)=C(q)/q pour tout q > 0.
a) Exprimer en fonction de q le coût unitaire moyen.

Réponse : CM(q)=C(q)/q = [ (q^3/3)-(6q^2)+40q ] / q = (q^2/3)-(6q)+40

b) Calculer le nombre q0 d’unités à fabriquer pour que le coût moyen soit minimal.

Réponse : on te demande de faire un tableau de variation
et de trouver la valeur de q telle que CM(q)= (q^2/3)-(6q)+40 soit minimal
et cette valeur est appelée dans cet exo :
IMPORTANT A RETENIR :
Ce qu'il faut comprendre c'est que la représentation graphique d'une fonction du second degré
comme la fonction définie par avec a,b et c 3 nombres donnés tels que
est une parabole dont le sommet est le point de la parabole d'abscisse
Dans ton message précédent :
tu as confondu la recherche de cette valeur pour la fonction CM définie par
avec le calcul de qui est l'image de par la fonction
ET n'est pas la valeur minimale prise par la fonction CM

2) On appelle coût marginal la dépense occasionnée par la production d’un objet supplémentaire. On modélise ce coût marginal par Cm(q) = C’(q) où C;) est la dérivée de C.
a) Exprimer en fonction de q le coût marginal.

Réponse : voir message précédent : Cm(q) = C’(q) = q^2-12q+40

b) Vérifier que pour q0, le coût marginal est égal au coût moyen.

Réponse: il faut calculer Cm et vérifier que cette valeur est égale à la notion de cout moyen
CONSEIL : regarde dans ton cours comment calculer un cout moyen

3) On suppose que l’entreprise vend toute sa production. Pour q E]0 ; 12] le bénéfice en centaines d’euros, pour la production de q milliers d’unités est B(q) = (-q^-3/3) + (2q^2) +21q
a) Calculer le nombre d’unités à produire pour que l’entreprise soit rentable.
b) Déterminer le nombre d’unités à fabriquer pour obtenir le bénéfice maximum. Que vaut ce bénéfice maximal ?

Réponse : Peux tu poser des questions sur ce que tu ne comprends pas ?

[dodie94]

Réponse : CM(q)=C(q)/q = [ (q^3/3)-(6q^2)+40q ] / q = (q^2/3)-(6q)+40

Réponse : on te demande de faire un tableau de variation
et de trouver la valeur de q telle que CM(q)= (q^2/3)-(6q)+40 soit minimal
et cette valeur est appelée dans cet exo :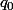
IMPORTANT A RETENIR :
Ce qu'il faut comprendre c'est que la représentation graphique d'une fonction du second degré
comme la fonction définie par avec a,b et c 3 nombres donnés tels que
est une parabole dont le sommet est le point de la parabole d'abscisse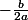
Dans ton message précédent :
tu as confondu la recherche de cette valeur pour la fonction CM définie par
avec le calcul de qui est l'image de par la fonction
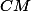
ET n'est pas la valeur minimale prise par la fonction CM
Réponse : voir message précédent : Cm(q) = C’(q) = q^2-12q+40
Réponse: il faut calculer Cm et vérifier que cette valeur est égale à la notion de cout moyen
CONSEIL : regarde dans ton cours comment calculer un cout moyen
Réponse : Peux tu poser des questions sur ce que tu ne comprends pas ?

Pour la question 2)b. cm(q0) ici c'est ce que j'avais fait non? si c'est cela je remplace q par 0 et le coût moyen c'est le coût total divisé par le nombre d'unités ou de personnes concernés par ce coût donc C(q)/q sauf que ce qu'on a trouver c'est (Q^2/3)-6q+40 donc bon je te le cache pas je suis un peu perdue la et dans le 3) je ne comprend pas quelle formule prendre pour pouvoir calculer le nombres d'unités pour que l'entreprise soit rentable et si on a besoin de la dérivée de B(q) c'est : q^2+4q+21 mais après ça j'ai aucune idée de comment je peux faire ... encore merci de m'aider ^^

[Anonyme]

Pour la question 2)b. cm(q0) ici c'est ce que j'avais fait non? si c'est cela je remplace q par 0 et le coût moyen c'est le coût total divisé par le nombre d'unités ^^

Réponse : Non ce n'est pas la bonne réponse : relis mon message précédent
et calcule comme je t'ai expliqué ...
On doit normalement trouver que pour cette valeur de :
que le coût marginal est égal au coût moyen c'est à dire à ??
Remarque :
je n'ai pas fait les calculs

dans le 3) je ne comprend pas quelle formule prendre pour pouvoir calculer le nombres d'unités pour que l'entreprise soit rentable et si on a besoin de la dérivée de B(q) c'est : q^2+4q+21 mais après ça j'ai aucune idée de comment je peux faire ... encore merci de m'aider ^^

Réponse :
a) on te demande de calculer la veleur de telle que C(q)=B(q)
b) on te demande d'étudier la fonction définie par quand
pour touver la valeur de où la fonction définie par a son minimum

[dodie94]

Réponse : Non ce n'est pas la bonne réponse : relis mon message précédent
et calcule comme je t'ai expliqué ...
On doit normalement trouver que pour cette valeur de :
que le coût marginal est égal au coût moyen c'est à dire à ??
Remarque :
je n'ai pas fait les calculs

Réponse :
a) on te demande de calculer la veleur de telle que C(q)=B(q)
b) on te demande d'étudier la fonction définie par quand
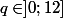
pour touver la valeur de où la fonction définie par a son minimum

jcrois j'ai compris est ce que pour la 1) b. faut faire q^2-12q+40=0 et développé? Autant pour moi c'est pas ça XD

[Anonyme]

jcrois j'ai compris est ce que pour la 1) b. faut faire q^2-12q+40=0 et développé?

NON la question 1.b) demande d'étudier la fonction CM(q)=(q^2/3)-(6q)+40 ( appelle la fonction f si cela t'aide ) quand ( appelle la variable x si cela t'aide )
ET donc

1) étudie la fonction f(x)=(x^2/3)-(6x)+40 quand
2) trace un tableau de variation de cette fonction pour trouver la valeur de qui rend cette fonction MINIMALE


ps)
Dans ton message tu as confondu CM(Q) et cm(q)
Essaie de faire ATTENTION à ce que tu comprends et écris

Conseil : essaie de RELIRE attentivement mes différents messages en écrivant ce que tu comprends sur une feuille (car tu confonds plusieurs notions)

Pour t'aider : voici une copie de l'un d'entre eux :

@dodie94

On a c(q)=(q^3/3)-(6q^2)+40q

1) calcul du coût unitaire moyen
CM(q)=C(q)/q = [ (q^3/3)-(6q^2)+40q ] / q = (q^2/3)-(6q)+40

2) calcul du coût marginal
Cm(q) = C’(q) = (u+v+w)'(q)

avec u(q)= q^3/3 et v(q)= -(6q^2) et w(q) = 40q

D'après des formules du cours on sait que
u'(q)= q^2
v'(q)=-12q
w'(q)=40
et que (u+v+w)'(q)=u'(q)+v'(q)+w'(q)

donc Cm(q) = C’(q) = q^2-12q+40

Essaie de continuer à travailler cet exo et n'hésite pas à poser d'autres questions


ps)
Dans cet exercice la variable des fonctions est
( au lieu généralement de )

Pour calculer des fonctions dérivées , on dérive par rapport à cette variable
( et cela revient à appliquer les formules du cours en remplaçant par )