Fonction dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
confetti
- Messages: 7
- Enregistré le: 27 Mar 2009, 19:51
-
 par confetti » 27 Mar 2009, 20:23
par confetti » 27 Mar 2009, 20:23
Bonjour, je suis en 1ere S et je suis bloquée dans mon DM
voilà mon problème :
Il faut que j'étudie la fonction
 = sqrt{a+x} {(\frac{1}{sqrt{a}} +{\frac{1}{sqrt{x}}))
avec a>o et x variable x>o
j'ai donc commencé par calculer la dérivée mais je coince. D'après mon prof je devrais trouver
= \frac{1}{2sqrt{a+x}} (\frac{1}{sqrt{a}}+\frac{1}{sqrt{x}})-\frac{sqrt{a+x}}{2x sqrt{x}})
mais pour l'instant je ne trouve que
= (\frac{1}{2sqrt{a+x}}) (\frac{1}{sqrt{a}}+\frac{1}{sqrt{x}})-\frac{a sqrt{a+x}+x sqrt{a+x}}{2 sqrt{x}})
j'ai appliqué U'V+V'U
Merci de bien vouloir m'aider
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 27 Mar 2009, 21:22
par uztop » 27 Mar 2009, 21:22
Bonjour,
oui, il faut bien appliquer (uv)' = u'v+v'u
Mais il y a une erreur de calcul dans ce que tu as fait: quelle est la dérivée de

?
-
confetti
- Messages: 7
- Enregistré le: 27 Mar 2009, 19:51
-
 par confetti » 28 Mar 2009, 11:02
par confetti » 28 Mar 2009, 11:02
j'ai retravaillé dessus et c'est justement la dérivée de

qui me pose problème
je ne sais pas s'il faut que j'utilise la fonction dérivée de :
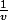
ou poser u(x)=
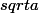
et
=\frac{1}{x})
j'utilise à ce moment là (
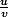
)' ça revient peut-être au même
dans mes calculs je trouve que la dérivée de

vaut

et

vaut

mais je n'arrive pas à me débarrasser de 2a
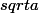
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 28 Mar 2009, 11:10
par uztop » 28 Mar 2009, 11:10
la variable est x dans ta fonction.

est donc une constante et sa dérivée est nulle.
-
confetti
- Messages: 7
- Enregistré le: 27 Mar 2009, 19:51
-
 par confetti » 28 Mar 2009, 11:23
par confetti » 28 Mar 2009, 11:23
Merci, je ne l'avais pas remarqué je vais refaire mes calculs.
Par contre j'ai encore une question, pour étudier le signe de f'(x) mon professeur nous a simplifié la fonction et ainsi il faut étudier le signe de h(x)=

on sait alors que f s'annule pour x=a
mais il faut alors trouver le signe de h lorsque x<a je n'ai pas compris comment il faut faire pourriez-vous encore m'aider ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 28 Mar 2009, 11:33
par uztop » 28 Mar 2009, 11:33
pour le passage de
-\frac{sqrt{a+x}}{2x sqrt{x}})
à

ton prof a simplement multiplié par

qui est toujours positif et ne change donc pas le signe de la fonction.
Pour étudier le signe de h(x), tu sais que h(a)=0. En étudiant le sens de variation de h (donc sa dérivée), tu pourras connaitre son signe (si h est croissante, elle sera négative pour x<a et inversement)
-
confetti
- Messages: 7
- Enregistré le: 27 Mar 2009, 19:51
-
 par confetti » 28 Mar 2009, 12:32
par confetti » 28 Mar 2009, 12:32
je viens de calculé h'(x) et je trouve

comme

est toujours positif
le signe de h'(x) dépend de x-3 or x-3=0 si x=3
j'en déduis que si x3 h'(x) est positive
est-ce la bonne réponse ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 28 Mar 2009, 13:22
par uztop » 28 Mar 2009, 13:22
il y a une erreur de calcul, comment est ce que les termes en

ont pu complètement disparaitre ?
Au moment de calculer la dérivée de

, il faut utiliser la formule
' = \frac{u'v-v'u}{v^2^})
-
confetti
- Messages: 7
- Enregistré le: 27 Mar 2009, 19:51
-
 par confetti » 28 Mar 2009, 15:25
par confetti » 28 Mar 2009, 15:25
j'ai utilisé cette formule
pour la dérivée de

je trouve

et pour la dérivée de

je trouve

ce résultat me paraissait juste puisque h(3)=0 lorsque x=a=3
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 28 Mar 2009, 15:47
par uztop » 28 Mar 2009, 15:47
oui mais pour la dérivée de

tu trouves quoi ?
Il faut appliquer la formule de la dérivée de
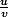
avec u=a+x et
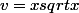
-
confetti
- Messages: 7
- Enregistré le: 27 Mar 2009, 19:51
-
 par confetti » 28 Mar 2009, 20:34
par confetti » 28 Mar 2009, 20:34
je trouve u'=1 et v'=3/2

et donc
}{x^3})

est-ce le bon résultat ?
-
soso008
- Messages: 7
- Enregistré le: 28 Mar 2009, 21:49
-
 par soso008 » 28 Mar 2009, 23:10
par soso008 » 28 Mar 2009, 23:10
oui cette dérivée est bonne! courage!tu peux continuer!
-
confetti
- Messages: 7
- Enregistré le: 27 Mar 2009, 19:51
-
 par confetti » 29 Mar 2009, 10:08
par confetti » 29 Mar 2009, 10:08
:id: j'ai alors mis les 2 membres sous le même dénominateur et je trouve alors :
h'(x) =

j'en déduis que h est croissante donc négative pour xa est-ce la bonne réponse ou est-ce que j'ai fait une erreur de calcul ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités