Fonction dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 19:28
par figueabricot » 29 Mar 2012, 19:28
figueabricot a écrit:EXTREMUM? c'est quoça me dit rien
aidez mo svp!
-
st00pid_n00b
- Membre Relatif
- Messages: 251
- Enregistré le: 03 Fév 2012, 19:54
-
 par st00pid_n00b » 29 Mar 2012, 19:29
par st00pid_n00b » 29 Mar 2012, 19:29
La dérivée d'une fonction te sert à trouver ses variations, c'est à dire le tableau avec les flèches qui montent, qui descendent, tout ça.
A partir du tableau tu dois ici trouver la valeur la plus grande de f (distance AI maximale). Ça s'appelle un maximum.
Donc déjà, commence par faire ce tableau.
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 19:31
par figueabricot » 29 Mar 2012, 19:31
st00pid_n00b a écrit:La dérivée d'une fonction te sert à trouver ses variations, c'est à dire le tableau avec les flèches qui montent, qui descendent, tout ça.
A partir du tableau tu dois ici trouver la valeur la plus grande de f (distance AI maximale). Ça s'appelle un maximum.
Donc déjà, commence par faire ce tableau.
je sais pas faire ça comment je sais?
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 19:34
par figueabricot » 29 Mar 2012, 19:34
figueabricot a écrit:je sais pas faire ça comment je sais?
monte moi comment faire
-
st00pid_n00b
- Membre Relatif
- Messages: 251
- Enregistré le: 03 Fév 2012, 19:54
-
 par st00pid_n00b » 29 Mar 2012, 19:35
par st00pid_n00b » 29 Mar 2012, 19:35
figueabricot a écrit:je sais pas faire ça comment je sais?
Tu as dû voir ça en cours normalement, sinon on te donnerait pas cet exo. Il faut étudier le signe de la dérivée, tu trouves quoi finalement pour la dérivée?
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 19:40
par figueabricot » 29 Mar 2012, 19:40
-(x-x^2)}{(x+1)^2})
mais j'ai vu ça qu une seul fois mais j'ai pas compris comment faire je te jure mon prof m'a dit qu on fait cet exos pour s entrainer pour l année prochaine mais c'est à rendre
-
st00pid_n00b
- Membre Relatif
- Messages: 251
- Enregistré le: 03 Fév 2012, 19:54
-
 par st00pid_n00b » 29 Mar 2012, 19:43
par st00pid_n00b » 29 Mar 2012, 19:43
C'est :
(x+1)-(x-x^2)}{(x+1)^2})
en faisant la dérivée de u/v. Après, il faut simplifier. Comment ça t'as pas appris, tu n'es pas en première?
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 19:46
par figueabricot » 29 Mar 2012, 19:46
figueabricot a écrit:-(x-x^2)}{(x+1)^2})
mais j'ai vu ça qu une seul fois mais j'ai pas compris comment faire je te jure mon prof m'a dit qu on fait cet exos pour s entrainer pour l année prochaine mais c'est à rendre
please aide moi svp
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 19:47
par figueabricot » 29 Mar 2012, 19:47
figueabricot a écrit:please aide moi svp
je suis en seconde
-
st00pid_n00b
- Membre Relatif
- Messages: 251
- Enregistré le: 03 Fév 2012, 19:54
-
 par st00pid_n00b » 29 Mar 2012, 19:51
par st00pid_n00b » 29 Mar 2012, 19:51
figueabricot a écrit:je suis en seconde
Ah, c'est une classe spéciale? Tu as bien vu les dérivées en cours? Normalement c'est au programme de première. Sinon, tu as simplifié l'expression de f'(x) ?
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 29 Mar 2012, 19:52
par globule rouge » 29 Mar 2012, 19:52
Oui, d'ailleurs St00pid N00b a bien fait de relever une erreur que j'ai faite sur le calcul de dérivée

La dérivée d'un quotient de deux fonctions u et v est le quotient
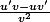
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 19:59
par figueabricot » 29 Mar 2012, 19:59
st00pid_n00b a écrit:C'est :
(x+1)-(x-x^2)}{(x+1)^2})
en faisant la dérivée de u/v. Après, il faut simplifier. Comment ça t'as pas appris, tu n'es pas en première?
)
pour la derivee reduite
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 20:01
par figueabricot » 29 Mar 2012, 20:01
figueabricot a écrit:)
pour la derivee reduite
-x^2-x sur (x+1)
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 20:02
par figueabricot » 29 Mar 2012, 20:02
figueabricot a écrit:-x^2-x sur (x+1)
y a une erreur ?
-
st00pid_n00b
- Membre Relatif
- Messages: 251
- Enregistré le: 03 Fév 2012, 19:54
-
 par st00pid_n00b » 29 Mar 2012, 20:08
par st00pid_n00b » 29 Mar 2012, 20:08
figueabricot a écrit:y a une erreur ?
Oui il y a une erreur, tu peux détailler tes calculs?
-
st00pid_n00b
- Membre Relatif
- Messages: 251
- Enregistré le: 03 Fév 2012, 19:54
-
 par st00pid_n00b » 29 Mar 2012, 20:11
par st00pid_n00b » 29 Mar 2012, 20:11
@globule: On va dire que c'était une faute de frappe ;)
Si tu veux prendre le relais des explications, y'a pas de soucis.
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 29 Mar 2012, 20:12
par globule rouge » 29 Mar 2012, 20:12
st00pid_n00b a écrit:@globule: On va dire que c'était une faute de frappe

Si tu veux prendre le relais des explications, y'a oas de soucis.
Non non, vas y ^^ Tu expliqueras mieux que moi !
-
figueabricot
- Membre Relatif
- Messages: 118
- Enregistré le: 08 Nov 2011, 20:42
-
 par figueabricot » 29 Mar 2012, 20:13
par figueabricot » 29 Mar 2012, 20:13
AI= x-x^2 sur x+1
C'est une fonvtion du type u sur v
u(x)=x-x^2 u'(x)=1-2x
v(x)=x+1 v'(x)=1
je suis perdue!
-
st00pid_n00b
- Membre Relatif
- Messages: 251
- Enregistré le: 03 Fév 2012, 19:54
-
 par st00pid_n00b » 29 Mar 2012, 20:20
par st00pid_n00b » 29 Mar 2012, 20:20
figueabricot a écrit:AI= x-x^2 sur x+1
C'est une fonvtion du type u sur v
u(x)=x-x^2 u'(x)=1-2x
v(x)=x+1 v'(x)=1
je suis perdue!
D'accord, donc en écrivant:
 = \frac{u'v - uv'}{v^2})
Ça te donne bien:
(x+1)-(x-x^2)}{(x+1)^2})
Maintenant, il faut développer et simplifier le numérateur.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités