Fonction dérivée

[globule rouge]

ok!

bon ça me

AI= x-x^2 sur x+1
C'est une fonvtion du type u sur v

u(x)=x-x^2 u'(x)=1
v(x)=x+1 v'(x)=1


donc f'(x)= (x-x^2) 1 - (x+1) 1 sur (x+1)^2

c'est bon?


comment tu fais pour mette les formule en latex?

Pour utiliser Latex, il faut écrire des formules ou une phrase en syntaxe particulière puis l'encadrer par des bornes spéciales. Je te renvoie à ce très bon topic d'uztop

La dérivée de est-elle 1 ????

[figueabricot]

ok!

bon ça me

AI= x-x^2 sur x+1
C'est une fonvtion du type u sur v

u(x)=x-x^2 u'(x)=1
v(x)=x+1 v'(x)=1


donc f'(x)= (x-x^2) 1 - (x+1) 1 sur (x+1)^2

c'est bon?


comment tu fais pour mette les formule en latex?

c'est pas bon?

[figueabricot]

Pour utiliser Latex, il faut écrire des formules ou une phrase en syntaxe particulière puis l'encadrer par des bornes spéciales. Je te renvoie à ce très bon topic d'uztop )

La dérivée de est-elle 1 ????

EUH VU TA QUESTION NON MAIS JE M EN RAPPELLE PLUS

DONNE LA MOI SOUS FORME DE LATTRE EXEMPLE AVEC A POUR QUE JE PUISSE LA TROUVER MOI MEME

[figueabricot]

EUH VU TA QUESTION NON MAIS JE M EN RAPPELLE PLUS

DONNE LA MOI SOUS FORME DE LATTRE EXEMPLE AVEC A POUR QUE JE PUISSE LA TROUVER MOI MEME

c'est vrai qu'il est pas mal ce topic

[figueabricot]

c'est vrai qu'il est pas mal ce topic

sous forme de lettre

[globule rouge]

EUH VU TA QUESTION NON MAIS JE M EN RAPPELLE PLUS

DONNE LA MOI SOUS FORME DE LATTRE EXEMPLE AVEC A POUR QUE JE PUISSE LA TROUVER MOI MEME

haha ^^
Bon, la dérivée d'une constante est 0
La dérivée d'une fonction affine (monôme) de type ax+b est a (b constante) puisque la dérivée de ax=a
La dérivée d'un trinôme du second degré de la forme ax²+bx+c avec a, b et c des constantes, est 2ax+b
Plus généralement, la dérivée d'un polynôme de la forme avec est le polynôme en appliquant la formule de dérivation

[figueabricot]

haha ^^
Bon, la dérivée d'une constante est 0
La dérivée d'une fonction affine (monôme) de type ax+b est a (b constante) puisque la dérivée de ax=a
La dérivée d'un trinôme du second degré de la forme ax²+bx+c avec a, b et c des constantes, est 2ax+b
Plus généralement, la dérivée d'un polynôme de la forme avec est le polynôme en appliquant la formule de dérivation

euh aide moi je comprend plus C EST 2x?

[figueabricot]

euh aide moi je comprend plus C EST 2x?

C d accord pour fb?

[globule rouge]

euh aide moi je comprend plus C EST 2x?

simplement, ton expression à dériver est
On sait que d'où , ok ?
Ici, et
On dérive x, ce qui vaut 1 et on dérive x² qui vaut ?

[figueabricot]

simplement, ton expression à dériver est
On sait que d'où , ok ?
Ici, et
On dérive x, ce qui vaut 1 et on dérive x² qui vaut ?

C'est bon?

[globule rouge]

C'est bon?

tu veux plutôt dire (x²)'=2x non ?

Au fait, pour ma boîte de messagerie, elle était pleine mais je viens de faire le ménage ^^

[figueabricot]

tu veux plutôt dire (x²)'=2x non ?

Au fait, pour ma boîte de messagerie, elle était pleine mais je viens de faire le ménage ^^

oui c'est ça

et donc t'es d accord pour fb


je fais comment pour la suite?

[globule rouge]

oui c'est ça

et donc t'es d accord pour fb


je fais comment pour la suite?

fb ? Qu'est-ce que tu veux dire par là ?
Et bien pour la suite, tu regardes mon message de 19h22 !

[figueabricot]

fb ? Qu'est-ce que tu veux dire par là ?
Et bien pour la suite, tu regardes mon message de 19h22 !

b) Déterminer la position du point E pour que la distance AI soit maximale.
2° Quelle est la position du point E qui rend l'aire du triangle AIE maximale?

je fais comment pour ça?

fb= facebook

[figueabricot]

je fais comment pour ça?

fb= facebook

b) Déterminer la position du point E pour que la distance AI soit maximale.
2° Quelle est la position du point E qui rend l'aire du triangle AIE maximale?

je fais comment pour la suite?

[globule rouge]

je fais comment pour ça?

fb= facebook

Ok, soit
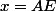
Nous voulons que soit minimale. Or, comment fait-on pour trouver x afin que AI soit minimale et en utilisant AI' ?

[figueabricot]

Ok, soit
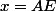
Nous voulons que soit minimale. Or, comment fait-on pour trouver x afin que AI soit minimale et en utilisant AI' ?

JE FAIS COMMENT JE SAIS PAS COMMENT REPONDRE A TA QUESTION

[globule rouge]

JE FAIS COMMENT JE SAIS PAS COMMENT REPONDRE A TA QUESTION

Sais-tu ce qu'est un extremum ? Quand une fonction f est continue et dérivable sur un intervalle, on localise généralement son extremum local au lieu où f' s'annule et change de signe.
Cela se traduit graphiquement par une fonction qui change de variations !

[figueabricot]

JE FAIS COMMENT JE SAIS PAS COMMENT REPONDRE A TA QUESTION

:we: POUR LA SUITE JE SAIS PAS FAIRE

[figueabricot]

Sais-tu ce qu'est un extremum ? Quand une fonction f est continue et dérivable sur un intervalle, on localise généralement son extremum local au lieu où f' s'annule et change de signe.
Cela se traduit graphiquement par une fonction qui change de variations !

EXTREMUM? c'est quoça me dit rien