Bonjour à tous.
Je dois résoudre l'équation suivante.
e^(2x-2) _ (1+e).e^(x) + e^3 = 0
L'ensemble de définition étant l'ensemble des réels R.
Comment faire ? Je me retrouve assez rapidement bloqué, et si j'obtiens un résultat, je doute de sa justese :mur:
Je fais :
e^(2x-2) + e^3 = (1+e).e^x
j'obtiens alors
(e^(2x-2))/(e^x) + e^3 = 1+e
c'est là que je ne suis pas sûre de moi car j'obtiens
e^x-2 + e^3 -e^1 = 1
ce qui équivaut à x-2+3-1-1 = 0
x= 2-3-2
x=1
Voila...
Si vous pouvez m'aider, merci beaucoup :help:
[Term S] Fonction dérivée.
4 messages
- Page 1 sur 1
Bonjour,
Je ne comprends pas trop ton bricolage ... si tu veux diviser l'égalité par , il faut diviser tout les termes ... Enfin ce n'est pas comme ca qu'il faut partir.
, il faut diviser tout les termes ... Enfin ce n'est pas comme ca qu'il faut partir.
Il faut tout d'abord te rappeler que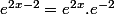 et que
et que 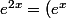^2) ... et ensuite tu utilise le changement de variable
... et ensuite tu utilise le changement de variable  et la ca devient plus agréable à regarder.
et la ca devient plus agréable à regarder.
Je ne comprends pas trop ton bricolage ... si tu veux diviser l'égalité par
Il faut tout d'abord te rappeler que
L'équation .e^x + e^3 = 0) s'écrit encore
s'écrit encore .(e^{x})^{2}-(1+e).e^{x} + e^3 = 0) Ce qui est une équation du second degré en X en posant
Ce qui est une équation du second degré en X en posant 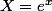 (on a alors X appartient à R+)
(on a alors X appartient à R+)
Tu résous en X cherche la racine POSITIVE puis passe au log...
Oboulo
"Utilisez le LATEX!!! Passer 3 plombes a comprendre vos notations laides et ambigues c'est NUUUUUL" (cri du coeur)
SI vous êtes sur Paris et avez besoin de cours, http://oboulo.e-monsite.com
Tu résous en X cherche la racine POSITIVE puis passe au log...
Oboulo
"Utilisez le LATEX!!! Passer 3 plombes a comprendre vos notations laides et ambigues c'est NUUUUUL" (cri du coeur)
SI vous êtes sur Paris et avez besoin de cours, http://oboulo.e-monsite.com
D'accord.
Je comprend. En effet mon bidouillage était incohérent.
Mais une fois que j'ai cette équation, je calcule le discriminant. Qui me donnerait alors
Delta = (1+e)^2 -4 e^(-2) . e^3
soit 1+2e+e^2 -4e^(-2+3)
1-2e + e^2
Ce qui donnerait donc
x1 = [ -1 -e + racine carrée de (1-2e +e^2 ) ] / 2.e^(-2)
Je comprend. En effet mon bidouillage était incohérent.
Mais une fois que j'ai cette équation, je calcule le discriminant. Qui me donnerait alors
Delta = (1+e)^2 -4 e^(-2) . e^3
soit 1+2e+e^2 -4e^(-2+3)
1-2e + e^2
Ce qui donnerait donc
x1 = [ -1 -e + racine carrée de (1-2e +e^2 ) ] / 2.e^(-2)
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
