Fonction cube niveau 1ereS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Mariondeguilhem
- Membre Naturel
- Messages: 45
- Enregistré le: 16 Sep 2006, 21:05
-
 par Mariondeguilhem » 16 Sep 2006, 21:16
par Mariondeguilhem » 16 Sep 2006, 21:16
1er dm de lannée en 1ere S
aidez moi!!
je seche!
soit g la fonction cube (definie sur R par g(x)=x au cube
verifiez que si a et b sont 2 réels alors
g(a)- g(b) = (a-b) ((a+b/2)²+ 3b²/4)
en deduire que si a est inferieur ou egal à b alord g(a) est inferieur ou egal à g(b)
quelles sont les variations de g?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 16 Sep 2006, 21:20
par abcd22 » 16 Sep 2006, 21:20
Bonsoir,
quelle est la question qui te pose problème ?
-
Mariondeguilhem
- Membre Naturel
- Messages: 45
- Enregistré le: 16 Sep 2006, 21:05
-
 par Mariondeguilhem » 16 Sep 2006, 21:24
par Mariondeguilhem » 16 Sep 2006, 21:24
bonsoir en fait, ttes.la plus difficile à mes yeux c'est la 1ere (verifiez ke a et b sont 2 réels)
je ne voit pa du tt.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 16 Sep 2006, 21:38
par abcd22 » 16 Sep 2006, 21:38
On demande juste de vérifier que
 \( \( a +\frac{b}{2} \)^2 + \frac{3b^2}{4} \)= a^3 - b^3)
, il suffit de développer ce qui est à gauche, de réduire, et de vérifier qu'on trouve bien

.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 16 Sep 2006, 21:50
par abcd22 » 16 Sep 2006, 21:50
Il n'y a pas de cube dans
\( \( a+ \frac{b}{2} \)^2 +\frac{3b^2}{4} \))
, tu peux partir de ça pour montrer l'égalité.
Sinon si tu tiens absolument à partir de
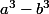
on a une identité remarquable
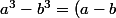(a^2 + ab + b^2))
, mais je ne sais pas si tu l'as vue et c'est plus simple de partir de
\( \( a+ \frac{b}{2} \)^2 +\frac{3b^2}{4} \))
.
-
Mariondeguilhem
- Membre Naturel
- Messages: 45
- Enregistré le: 16 Sep 2006, 21:05
-
 par Mariondeguilhem » 16 Sep 2006, 22:07
par Mariondeguilhem » 16 Sep 2006, 22:07
je n'arrive pas a develloper avec les fractions....
en tout cas, je vous remercie enormement pour votre aide, j'y vois bcp plus clair! merci infiniment!
ce site est super! je viens juste de le decouvrir mais c'est le bonheur!
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 16 Sep 2006, 22:20
par abcd22 » 16 Sep 2006, 22:20
On utilise l'identité remarquable (x+y)² = x² + 2xy + y², on trouve
^2 = a^2 + ab + \(\frac{b}{2}\)^2 = a^2 + ab + \frac{b^2}{4})
, ce n'est pas plus difficile que sans fractions.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 16 Sep 2006, 22:46
par abcd22 » 16 Sep 2006, 22:46
Euh c'est du niveau collège les calculs pourtant, il n'y a rien à comprendre, il faut juste connaître une identité remarquable et les règles de calcul avec les fractions...
-
Mariondeguilhem
- Membre Naturel
- Messages: 45
- Enregistré le: 16 Sep 2006, 21:05
-
 par Mariondeguilhem » 16 Sep 2006, 22:49
par Mariondeguilhem » 16 Sep 2006, 22:49
j'ai jamias fait le programme en math ce qui m'embete le plus ce sont les carrés
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 16 Sep 2006, 23:15
par abcd22 » 16 Sep 2006, 23:15
Qu'est-ce que tu trouves ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
