Fonction continue
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 22 Sep 2007, 14:15
par Imod » 22 Sep 2007, 14:15
Pour

positif :
(\sqrt{x}+3))
Imod
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 14:16
par gol_di_grosso » 22 Sep 2007, 14:16
faut que tu définissent f(9)
pour qu'elle soit continue y faut que la limite à gauche et la limite à droite en 9 soit egal
en gros calcule les limites de f quan x tend vers 9 par en dessous et par en dessus si c la meme limite celle ci est égale à L
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 14:21
par gol_di_grosso » 22 Sep 2007, 14:21
faut utiliser ce qu'a dit imod pour le faire
-
toto_tom
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Sep 2006, 19:29
-
 par toto_tom » 22 Sep 2007, 16:32
par toto_tom » 22 Sep 2007, 16:32
Bonjour. J'ai le même exercice. Donc si on transforme x-9, f(x) devient
18-6racine de x / ((racine de x )-3)((racine de x) +3).
Mais la limite donne toujours 0/0 donc FI.
On doit pouvoir factoriser non en mettant 3 en facteur?
Moi ej n'y arrive pas
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 22 Sep 2007, 16:47
par Imod » 22 Sep 2007, 16:47
Pour
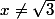
, on a
=\frac{6(3-\sqrt{x})}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{-6}{\sqrt{x}+3})
, je te laisse finir .
Imod
-
toto_tom
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Sep 2006, 19:29
-
 par toto_tom » 22 Sep 2007, 19:09
par toto_tom » 22 Sep 2007, 19:09
Ahh! J'y étais presque j'avais factorisé par 3. Effectivement par 6 c'était plus efficace!
Donc f(9)=-1 et les limites quand x tend vers 9 sont -1 aussi c'est ça?
Donc la valeur de L pour que f soit continue est -1.
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 19:37
par gol_di_grosso » 22 Sep 2007, 19:37
enfaite maintenant tu defini f comme ça :
c'est
 = \frac {18-6sqrt{x}} {x-9} x \in \R \not= {} 9 \\ f(9) = -1)
-
toto_tom
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Sep 2006, 19:29
-
 par toto_tom » 22 Sep 2007, 20:01
par toto_tom » 22 Sep 2007, 20:01
Merci beaucoup pour votre aide.
Nous avons une 2e question, si c'est possible que vous nous aidiez.
2)Soit la fonction g définie sur [0;+inf[ par
g(x)=sin2x/(2x-pi) si x différent de pi/2
g(pi/2)=-1
Démontrer que la fonction g est continue sur [0;+inf[
Je pense qu'il faut étudier la limite de g(x) quand x tend vers pi/2.
J'avais pensé à d'abord réécrire g(x) :
g(x)=2sinxcosx/2x-pi
Mais bon pour trouver la limite c'est un autre problème. Suis-je bien parti?
-
toto_tom
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Sep 2006, 19:29
-
 par toto_tom » 22 Sep 2007, 20:27
par toto_tom » 22 Sep 2007, 20:27
Pardon jéjouille?
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 20:37
par gol_di_grosso » 22 Sep 2007, 20:37
toto_tom a écrit:Merci beaucoup pour votre aide.
Nous avons une 2e question, si c'est possible que vous nous aidiez.
2)Soit la fonction g définie sur [0;+inf[ par
g(x)=sin2x/(2x-pi) si x différent de pi/2
g(pi/2)=-1
Démontrer que la fonction g est continue sur [0;+inf[
Je pense qu'il faut étudier la limite de g(x) quand x tend vers pi/2.
ouai par en dessous et par en dessus
a savoir la limite est
-1 c logique vu que c dans l"énoncé bref selectionne c ecrit en blanc
-
toto_tom
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Sep 2006, 19:29
-
 par toto_tom » 22 Sep 2007, 20:46
par toto_tom » 22 Sep 2007, 20:46
Pour le calcul de la limite de g(x) ça me donne 0+/0- donc un FI.
Que puis-je faire?
Je sais que sin2x=2sinxcosx ça peut peut-être m'aider non?
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 20:56
par gol_di_grosso » 22 Sep 2007, 20:56
change de variable et c'est facile
tu pose x=t+pi/2 t=x-pi/2 et ainsi quand x-> p/2 ,t->0
et repart de (sin(2x)/(2x+pi)
tu simplifie utilise sin(a+b)=...
et tu connais lim sin(t)/t quand t->0 non?
Je sais que sin2x=2sinxcosx ça peut peut-être m'aider non?
nan :hum:
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 21:03
par gol_di_grosso » 22 Sep 2007, 21:03
t'a lu en dessus ?????? :hum:
:triste: :we: :dodo:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
