Fonction complexe (z)

[Glueguy]

Bonjour, j'ai besoin de votre aide pour un DM traitant d'une fonction complexe.
Cela fait presque deux semaine que j'essaye régulièrement et rien a faire, je ne trouve rien

Donc voilà l'idée :
On a une fonction f(z) = ((3+4i)(x-iy)+4-8i) / 5

On doit trouver l'ensemble des points E du plan complexe telles que f(z)=z
(Sachant que z =x + iy )

Merci d'avance pour votre aide, n'hésitez pas a donner une méthode si jamais ;D

[infernaleur]

Salut, ton équations est équivalente à :
Ensuite tu peux développer et identifier partie réelle et partie imaginaire.

[Glueguy]

Donc, si je développe j'obtiens :
3x - 3iy +4ix+4y+4-8i = 5x+5iy
Donc je passe 5x+5iy de l'autre cote et j'ai :
-2x - 8iy + 4ix + 4y + 4 - 8i = 0
Et donc la, la partie imaginaire c'est ce qui dépend de i et la partie réelle c'est le reste (je crois)
Mais j'en fais quoi après ?

[infernaleur]

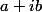
Un nombre complexe (c'est-à-dire un nombre de la forme avec a et b des réels) est nul si et seulement si sa partie réelle (ici a) et sa partie imaginaire (ici b) sont nulles.
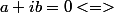
Donc ET .

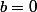
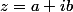
Plus généralement si tu as deux nombres complexes et .
ET

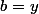
[Glueguy]

Donc pour que -2x - 8iy + 4ix + 4y + 4 - 8i = 0
Il faut que sa partie imaginaire (8iy+4ix-8i) soit égale a 0
Et que sa partie réelle (-2x+4y+4) soit égale a 0
Et la je fais un système c'est ça ?

[infernaleur]

Relis bien ce que j'ai écris,
déjà pour pouvoir utiliser ce que je t’ai dit, il faut que ça soit de la forme A+iB avec A et B des réels !!!!! Ici ce n'est pas le cas... Donc tu dois travailler un petit peu l'expression pour te ramener a une forme A+iB.
(8iy+4ix-8i) n'est pas un nombre réel donc tu peux pas utiliser ce que j'ai dit.

[Glueguy]

Oui mais pour obtenir des réelles il faudrait savoir combien vaut x et combien vaut y, et ça j'y arrive pas du tout...
Ou alors tu veux dire qu'il faut factoriser la partie imaginaire par i ?

[infernaleur]

Oui mais pour obtenir des réelles il faudrait savoir combien vaut x et combien vaut y, et ça j'y arrive pas du tout...

Bha x et y sont des réels pas la peine de savoir ce qu'ils valent

Ou alors tu veux dire qu'il faut factoriser la partie imaginaire par i ?

oui exactement comme ça tu auras un truc du type A+iB.

[Glueguy]

Ah d'accord j'y pensais mais du coup je me demandais si ca bloquerait pas avec x et y
Du coup on a
-2x - 8iy + 4ix + 4y + 4 - 8i = 0. <=>. -2x+4y+4 = 0. ET. 8y+4x-8 = 0
Et la on a un système ?

[infernaleur]

Oui mais en fait les deux équations sont équivalentes (tu multiple par -2) donc ton ensemble E c'est la droite d'équations -2x+4y+4=0

[Glueguy]

Oh ! Hé bien merci beaucoup pour votre aide infernaleur ! J'ai compris