Fonction : 2nde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dr Neurone
- Membre Complexe
- Messages: 2875
- Enregistré le: 17 Nov 2007, 19:03
-
 par Dr Neurone » 12 Déc 2007, 19:50
par Dr Neurone » 12 Déc 2007, 19:50
Juliadu59 a écrit:? je comprend pas la vous m'avez pas répondu a mon probleme , je reexplique :hum:
apres avoir fait
f(x) - (-2) j'avais obtenu une identité remarquable : (x-2)² et apartir de la comme vous dites ça doit tjrs etre positif ou nul mais si jamais c'est superieur a -2 ça peut faire -1 ! hors -1-2 ça donne -3 et -3 est negatif ..
Un carre est sup ou égal à 0 , pas à un nombre négatif comme le -1 que tu me proposes.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Déc 2007, 19:51
par raito123 » 12 Déc 2007, 19:51
Franchement non ce n'est pas ça:
tu ne doit pas écrire -(-2) parce que c'est impossible d'y ressortir une identit" remarquable ce qu'il faut faire c'est de d'ajouter un 2 et le retrancher pour que la fonction ne change pas :
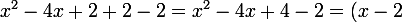^2-1)
Les multiples ne doivent pas être utilisés sans nécessité
-
Juliadu59
- Membre Naturel
- Messages: 49
- Enregistré le: 29 Avr 2007, 00:13
-
 par Juliadu59 » 12 Déc 2007, 19:59
par Juliadu59 » 12 Déc 2007, 19:59
je comprend pas m****
bon je vous ecris ce que j'ai mis :
f(x) - (-2) car il faut démontrer que f(x) > ( ou égal ) a -2 donc je soustrais pour comparer
je remplace donc f(x)
x²-4x+2 -(-2)
x²-4x+2+2
x²-4x+4
et la je retrouve une identité remarquable :
(x-2)² et la je suis completement bloqué apartir de la je sais pas ce que je dois faire

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Déc 2007, 20:01
par raito123 » 12 Déc 2007, 20:01
Ouais j'ai compris ce que tu voulais dire, c'est juste!
Les multiples ne doivent pas être utilisés sans nécessité
-
Juliadu59
- Membre Naturel
- Messages: 49
- Enregistré le: 29 Avr 2007, 00:13
-
 par Juliadu59 » 12 Déc 2007, 20:02
par Juliadu59 » 12 Déc 2007, 20:02
ok et apartir de sa je sais pas ce que je dois faire pour prouver que f(x) est bien egal ou superieur a -2
-
Dr Neurone
- Membre Complexe
- Messages: 2875
- Enregistré le: 17 Nov 2007, 19:03
-
 par Dr Neurone » 12 Déc 2007, 20:05
par Dr Neurone » 12 Déc 2007, 20:05
Juliadu59 a écrit:je comprend pas m****
bon je vous ecris ce que j'ai mis :
f(x) - (-2) car il faut démontrer que f(x) > ( ou égal ) a -2 donc je soustrais pour comparer
je remplace donc f(x)
x²-4x+2 -(-2)
x²-4x+2+2
x²-4x+4
et la je retrouve une identité remarquable :
(x-2)² et la je suis completement bloqué apartir de la je sais pas ce que je dois faire
Eh bien c'est bon? Ho ho ! mais dites donc , y'a pas marqué bécasse là !
x²-4x+4 > ( ou égal ) 0
donc en partant de la tu reviens à l'envers sur f(x) > ( ou égal ) a -2

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Déc 2007, 20:06
par raito123 » 12 Déc 2007, 20:06
bah rien puisque
^2)
est bel et bien positive alors f(x)>-2
et tu peux mettre ce que tu viens d'ecrire sur l'autre post dans ton brouillon et dans la copie tu met
^2>0)
et tu dévelppe
Les multiples ne doivent pas être utilisés sans nécessité
-
Juliadu59
- Membre Naturel
- Messages: 49
- Enregistré le: 29 Avr 2007, 00:13
-
 par Juliadu59 » 12 Déc 2007, 20:12
par Juliadu59 » 12 Déc 2007, 20:12
ok donc apres dans ma copie je mettrais :
(x-2)² est positif donc f(x) > ou egal a -2 ?
Merci d'avoir pris tous ce temps pour moi
-
Dr Neurone
- Membre Complexe
- Messages: 2875
- Enregistré le: 17 Nov 2007, 19:03
-
 par Dr Neurone » 12 Déc 2007, 20:13
par Dr Neurone » 12 Déc 2007, 20:13
Juliadu59 a écrit:ok donc apres dans ma copie je mettrais :
(x-2)² est positif donc f(x) > ou egal a -2 ?
Merci d'avoir pris tous ce temps pour moi
A ta santé , je m'en ressert un petit dernier !

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Déc 2007, 20:26
par raito123 » 12 Déc 2007, 20:26
Dr Neurone a écrit:A ta santé , je m'en ressert un petit dernier !
hey c'est à moi qu'elle l'a dit lol prenez le pas au serieux.
donc Juliadu59 tu developpe l'identité remarquable superieur ou egal à 0
(x-2)²>=0 et 0 la fin tu obtiendra ton résultat
Les multiples ne doivent pas être utilisés sans nécessité
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
