[Spé Maths] Fermat

[Drakula]

Bonsoir j'ai besoin d'aide pour cet exercice,

Econcé:


Ce que j'ai fais:

1)



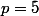
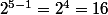
donc ainsi,

Vraie pour




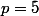
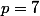
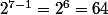
donc ainsi,

Vraie pour

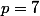
2) Si n est un multiple de k, on peut écrire n = k*q




Mon résultats sont bons ?

Je bloque à partir de la 3)a) .. Je sais qu'un nombre impair s'écrit de la forme 2k+1, mais je ne vois pas par où commencer.

Merci de vos réponses.

[Drakula]

J'ai continué à faire la 3a) est-ce que c'est bon ?

p est un nombre premier autre que 2, de plus est pair or = N donc N est un nombre impair.
p ne peut pas être égal à 2, de plus 2 est le seul nombre premier pair, donc p est forcément impair.

p est un diviseur premier N on peut donc écrire

soit,


b)

n=b*q+r avec 0<r<b




Donc

Comme 0<r<b et vérifie
r doit etre égal à 0 ainsi n=b*q donc n multiple de b.

Hmm bloqué à la 2c)

[Tiruxa]

Le début est juste, mais par la suite la rédaction avait besoin de quelques corrections (en rouge ci-dessous)

p est un nombre premier autre que 2, Attention ceci n'est pas une hypothèse ! à supprimer

est pair or N=2^17-1 donc N est un nombre impair.
p ne peut pas être égal à 2, de plus 2 est le seul nombre premier pair, donc p est forcément impair.

p est un diviseur premier N on peut donc écrire

soit,
il y avait un 1 en trop

b)

n=b*q+r avec 0<=r<b


après correction

or
Donc

Comme 0<=r<b et vérifie
r doit etre égal à 0 car b est le plus petit entier strictement positif vérifiant cette propriété
ainsi n=b*q donc n multiple de b.