Factoriser une equation du second degré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 15:55
par lo_hak95 » 13 Nov 2006, 15:55
Bonjours à tous,
Pouriez vous m'aider à factoriser cette équation:
X²-5x-14
je suis bloqué à la factorisation pour poursuivre mon exercice
merci d'avance
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 16:01
par fonfon » 13 Nov 2006, 16:01
Salut, tu es en quelle classe?
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:02
par lo_hak95 » 13 Nov 2006, 16:02
j'avai trouvé une solution mais je voudrais savoir
si on peut encore factorisé
X(x - 5 - 14/X)
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:03
par lo_hak95 » 13 Nov 2006, 16:03
fonfon a écrit:Salut, tu es en quelle classe?
je suis en BTS
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 16:05
par fonfon » 13 Nov 2006, 16:05
Re,
En reflechissant j'ai trouvé une solution mais je voudrais savoir
si on encore factorisé
X(x - 5 - 14/X)
ça ne te menera pas à grand chose en BTS tu as du voir la methode du discriminant je pense
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:12
par lo_hak95 » 13 Nov 2006, 16:12
fonfon a écrit:Re,
ça ne te menera pas à grand chose en BTS tu as du voir la methode du discriminant je pense
oui , en fait j'ai la fonction : f(t)=(8t-11)/(t²-5t-14)
en a/ on me demande de factoriser l'expression t²-5t-14
et en B/ on me demande de montrer qu'il existe des réel a et b tel que, pour tout t de I on a f(t) = a/(t+2) + b/(t-7)
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 16:15
par fonfon » 13 Nov 2006, 16:15
oui, mais pour la 1ere as-tu utilisé le discriminant ?
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:18
par lo_hak95 » 13 Nov 2006, 16:18
fonfon a écrit:oui, mais pour la 1ere as-tu utilisé le discriminant ?
quand tu di discriminant tu veut dire a(x-x1)(x-x2)
c'est sa??
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 16:24
par fonfon » 13 Nov 2006, 16:24
oui un polynôme du secon degré est une expression de la forme ax²+bx+c (a,b,c réels, a#0)
pour factoriser ce polynome on va chercher les racines du polynôme
on pose
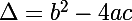
si
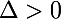
le polynôme a deux racines distinctes :
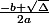
ou
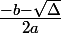
si
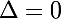
une racine double

si

pas de racines dans R
donc à toi d'appliquer
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:31
par lo_hak95 » 13 Nov 2006, 16:31
je suis trop bete je n'avais meme pas penser a utiliser delta merci
ce qui me donne 25-4*1*-14
25+56
81 d'où racine de delta = 9
x1= (5+9)/2 =14/2 =7
x2=(-5+9)/2 =4/2 = 2
ce qui donne en applicant a(x-x1)(x+x2)
donc le résultat (x-7)(x+2)
merci beaucoup de ton aide fonfon
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:46
par lo_hak95 » 13 Nov 2006, 16:46
lo_hak95 a écrit:oui , en fait j'ai la fonction : f(t)=(8t-11)/(t²-5t-14)
en a/ on me demande de factoriser l'expression t²-5t-14
et en B/ on me demande de montrer qu'il existe des réel a et b tel que, pour tout t de I on a f(t) = a/(t+2) + b/(t-7)
pourais tu m'aider pour la deuxieme question??
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:47
par lo_hak95 » 13 Nov 2006, 16:47
lo_hak95 a écrit:oui , en fait j'ai la fonction : f(t)=(8t-11)/(t²-5t-14)
en a/ on me demande de factoriser l'expression t²-5t-14
et en B/ on me demande de montrer qu'il existe des réel a et b tel que, pour tout t de I on a f(t) = a/(t+2) + b/(t-7)
pourai tu m'aider pour la 2 e question?
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:48
par lo_hak95 » 13 Nov 2006, 16:48
lo_hak95 a écrit:oui , en fait j'ai la fonction : f(t)=(8t-11)/(t²-5t-14)
en a/ on me demande de factoriser l'expression t²-5t-14
et en B/ on me demande de montrer qu'il existe des réel a et b tel que, pour tout t de I on a f(t) = a/(t+2) + b/(t-7)
pourai tu m'aider pour la 2eme question??
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 16:51
par fonfon » 13 Nov 2006, 16:51
reduis dejà au même denominateur tu va peut-être trouver par toi même
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 16:57
par lo_hak95 » 13 Nov 2006, 16:57
fonfon a écrit:reduis dejà au même denominateur tu va peut-être trouver par toi même
c'est ce que j'ai fait sa me donne
j'ai remplacé linconnu t par x
(ax-7a+bx+2b)/(x²-5x-14)
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 17:03
par fonfon » 13 Nov 2006, 17:03
donc comme on veut que:
f(x)=((a+b)x-7a+2b)/(x²-5x-14)
<=>
(8x-11)/(x²-5x-14)=((a+b)x-7a+2b)/(x²-5x-14)
il ne reste plus qu'a identifier les coefficient des termes de même degrè
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 17:13
par lo_hak95 » 13 Nov 2006, 17:13
fonfon a écrit:donc comme on veut que:
f(x)=((a+b)x-7a+2b)/(x²-5x-14)
(8x-11)/(x²-5x-14)=((a+b)x-7a+2b)/(x²-5x-14)
il ne reste plus qu'a identifier les coefficient des termes de même degrè
si je suis ce que tu me dit on se retrouve avec
(ax-7a²+2ba+bx-7ab+2b²)/(x²-5x-14)
n'y a t'il pas un probleme??
je pense plutot que (a(x-7)+b(x+2))/(x²-5x-14)
(8x-1)/(x²-5x-14)
d'où 8x-1 = a(x-7)+b(x+2)
ou 8x-1 = ax-7a+bx+2b
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 17:21
par fonfon » 13 Nov 2006, 17:21
houla, c'est pas ça je t'ai dit qu'il faut proceder à une identification
Rappel:
2 polynôme sont egaux ssi ils ont le même degrè avec les coefficients des termes de même defrè egaux donc ici pour identifier il suffit de resoudre:
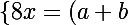x\\-11=-7a+2b)
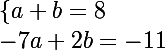
-
lo_hak95
- Membre Naturel
- Messages: 30
- Enregistré le: 13 Nov 2006, 15:50
-
 par lo_hak95 » 13 Nov 2006, 17:33
par lo_hak95 » 13 Nov 2006, 17:33
donc a=8-b
et on sait que -7a+2b=-11
donc -7(8-b)+2b=-11
-56+7b+2b=-11
9b=56-11
9b=45
d'où b=5
donc a = 3
Merci,merci merci fonfon grace a toi je vais pouvoir poursuivre mon exo et calculer mon integrale cool !!!
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 17:34
par fonfon » 13 Nov 2006, 17:34
oui c'est ça :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
