Bonjour, pourriez vous m'aider merci.
Après avoir effectué les calculs nécessaires, ( développements, réduction au même dénominateur) indiquer si les fonction suivantes sont des fonctions affines
f1(x) = 4x²-x-(2x-1)(2x+1) f2(x) = (3+x)(5-x)+1/2(3-x)
f3(t) = 2t-5/3 -3t/2 f4(u) = (3u-2)²-(3u-5) (3u+5)
voilà ce que j'ai fais
1(x) = 4x²-x-(2x-1)(2x+1) f2(x) = (3+x)(5-x)+1/2(3-x)
f(x) = 4x²-x-(4x²+2x-2x-1) f2(x) = 15-3x+5x-x+ 3/2-1x/2
f(x) = 16x²-x-4x²-2x+2x+1 Je bloque après
f(x) = 12x²-1x+1
Donc non
Factorisations / développements
12 messages
- Page 1 sur 1
Salut !
J'ai du mal à comprendre tout ce que tu as écrit : c'est pas très bien ordonné.
Mais si j'ai bien compris, tu te trompes : est affine (tu as fait apparaître un
est affine (tu as fait apparaître un 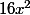 ...)
...)
Nana55 a écrit:Bonjour, pourriez vous m'aider merci.
Après avoir effectué les calculs nécessaires, ( développements, réduction au même dénominateur) indiquer si les fonction suivantes sont des fonctions affines
f1(x) = 4x²-x-(2x-1)(2x+1) f2(x) = (3+x)(5-x)+1/2(3-x)
f3(t) = 2t-5/3 -3t/2 f4(u) = (3u-2)²-(3u-5) (3u+5)
voilà ce que j'ai fais
1(x) = 4x²-x-(2x-1)(2x+1) f2(x) = (3+x)(5-x)+1/2(3-x)
f(x) = 4x²-x-(4x²+2x-2x-1) f2(x) = 15-3x+5x-x+ 3/2-1x/2
f(x) = 16x²-x-4x²-2x+2x+1 Je bloque après
f(x) = 12x²-1x+1
Donc non
J'ai du mal à comprendre tout ce que tu as écrit : c'est pas très bien ordonné.
Mais si j'ai bien compris, tu te trompes :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
voilà ce que j'ai fais
f(x) = 4x²-x-(2x-1)(2x+1)
f(x) = 4x²-x-(4x²+2x-2x-1)
f(x) = 16x²-x-4x²-2x+2x+1
f(x) = 12x²-1x+1
Ce résultat est-il juste? Mais affine il y a que 2 chiffres pas 3
f2(x) = (3+x)(5-x)+1/2(3-x)
f2(x) = 15-3x+5x-x+ 3/2-1x/2
La j'arrive pas à continuer pourriez vous m'aider s'il vous plait merci
f3(t) = 2t-5/3 -3t/2
=2t-5*2/3*2 - 3t*3/2*3
=2t-10/6 - 9t/6
= -7t-10/6
C'est bon? c'est pas affine
f4(u) = (3u-2)²-(3u-5) (3u+5)
= (3u)²-2*3u*2+2² (-3u)²-5²
= 9u²-12u+4+9u²-25
= 18u²-12u-21
C'est bon?
f(x) = 4x²-x-(2x-1)(2x+1)
f(x) = 4x²-x-(4x²+2x-2x-1)
f(x) = 16x²-x-4x²-2x+2x+1
f(x) = 12x²-1x+1
Ce résultat est-il juste? Mais affine il y a que 2 chiffres pas 3
f2(x) = (3+x)(5-x)+1/2(3-x)
f2(x) = 15-3x+5x-x+ 3/2-1x/2
La j'arrive pas à continuer pourriez vous m'aider s'il vous plait merci
f3(t) = 2t-5/3 -3t/2
=2t-5*2/3*2 - 3t*3/2*3
=2t-10/6 - 9t/6
= -7t-10/6
C'est bon? c'est pas affine
f4(u) = (3u-2)²-(3u-5) (3u+5)
= (3u)²-2*3u*2+2² (-3u)²-5²
= 9u²-12u+4+9u²-25
= 18u²-12u-21
C'est bon?
Nana55 a écrit:voilà ce que j'ai fais
f(x) = 4x²-x-(2x-1)(2x+1)
f(x) = 4x²-x-(4x²+2x-2x-1)
f(x) = 16x²-x-4x²-2x+2x+1
f(x) = 12x²-1x+1
Ce résultat est-il juste? Mais affine il y a que 2 chiffres pas 3
f2(x) = (3+x)(5-x)+1/2(3-x)
f2(x) = 15-3x+5x-x+ 3/2-1x/2
La j'arrive pas à continuer pourriez vous m'aider s'il vous plait merci
f3(t) = 2t-5/3 -3t/2
=2t-5*2/3*2 - 3t*3/2*3
=2t-10/6 - 9t/6
= -7t-10/6
C'est bon? c'est pas affine
f4(u) = (3u-2)²-(3u-5) (3u+5)
= (3u)²-2*3u*2+2² (-3u)²-5²
= 9u²-12u+4+9u²-25
= 18u²-12u-21
C'est bon?
Quelle est ta définition d'une fonction affine ?
Non, le premier est faux : elle est bien affine.
Si tu veux vérifier, tu peux toujours calculer pour des valeurs qui facilite les calculs : calcule f(1) avec l'expression donnée dans l'énoncé et ce que tu trouves, il y aura deux valeurs distinctes (ce qui prouve que ton égalité est fausse).
Comment passe-tu de l'égalité "f(x)=4x²-x-(4x²+2x-2x-1)" à l'égalité "f(x)=16x²-x-4x²-2x+2x+1" ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Nana55 a écrit:Tout se que j'ai fais est faux? Ben 4x² fait 16x² à mince il faut faire (2x-1)(2x+1)= (2x)²-1²
= 4x²-1
Non :
(2x-1)(2x+1)= (2x)²-1 = 4x²-1 est un moyen assez facile, rapide et malin de parvenir au bon résultat :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
f(x)= 4x²-x-4x²-2x+2x+1
f(x) =-x+1
f2(x) = 15-3x+5x-x²+3/2-1x/2
f2(x) = 15+3/2-3x+5-x²-1x/2
f2(x) = 33/2-3x+5x-x²-1x/2
f2(x) =33/2-x²+5x-3x -1x/2.
f2(x) = 33/2-x²+5x-6x+3x²
f2(x)= 4x²-1x+33/2
f3(t) = 2t -5/3 -3t/2
f3(t) = 2t-3t/2-5/3
f3(t) = (2-3/2)t -5/3
f3(t) = (1/2)t-5/3
f3(t) = 1/2x-5/3
f4(u) = (3u-2)²-(3u-5) (3u+5)
= (3u)²-2*3u*2+2²-(3u)²-5²
= 9u²-12u+4-9u²-25
= -12u-21
voilà
f(x) =-x+1
f2(x) = 15-3x+5x-x²+3/2-1x/2
f2(x) = 15+3/2-3x+5-x²-1x/2
f2(x) = 33/2-3x+5x-x²-1x/2
f2(x) =33/2-x²+5x-3x -1x/2.
f2(x) = 33/2-x²+5x-6x+3x²
f2(x)= 4x²-1x+33/2
f3(t) = 2t -5/3 -3t/2
f3(t) = 2t-3t/2-5/3
f3(t) = (2-3/2)t -5/3
f3(t) = (1/2)t-5/3
f3(t) = 1/2x-5/3
f4(u) = (3u-2)²-(3u-5) (3u+5)
= (3u)²-2*3u*2+2²-(3u)²-5²
= 9u²-12u+4-9u²-25
= -12u-21
voilà
Nana55 a écrit:f(x)= 4x²-x-4x²-2x+2x+1
f(x) =-x+1
f2(x) = 15-3x+5x-x²+3/2-1x/2
f2(x) = 15+3/2-3x+5-x²-1x/2
f2(x) = 33/2-3x+5x-x²-1x/2
f2(x) =33/2-x²+5x-3x -1x/2.
f2(x) = 33/2-x²+5x-6x+3x²
f2(x)= 4x²-1x+33/2
f3(t) = 2t -5/3 -3t/2
f3(t) = 2t-3t/2-5/3
f3(t) = (2-3/2)t -5/3
f3(t) = (1/2)t-5/3
f3(t) = 1/2x-5/3
f4(u) = (3u-2)²-(3u-5) (3u+5)
= (3u)²-2*3u*2+2²-(3u)²-5²
= 9u²-12u+4-9u²-25
= -12u-21
voilà
A vu d'oeil, ça à l'air bon.
Du coup, tu peux en déduire les fonctions qui sont affines.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Nana55 a écrit:f(x) et f4(u) sont affines les autres non
Revois ta définition d'une fonction affine :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Nana55 a écrit:Ah oui mince merci beaucoup
De rien :we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
