Factorisation

[nix2016]

Bonjour à tous
la question est toute simple j ai pas réussi a trouver
factoriser l expression suivante :

merci

[Lostounet]

Salut

Tu es sûr que c'est x^3-x^2+6 +qu'il faut factoriser?

[laetidom]

Bonsoir,

Exemple :

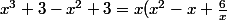Oui, l'énoncé est-il juste ? Car je ne vois pas beaucoup l'intérêt de la chose . . . ! ? . . .

[nix2016]

j été sur qu elle n avais pas de solution c est dans le manuel scolaire pour les eleves de la 1ere année secondaire jj ai essayé de voir x au cube + 2 au cube en ajoutant et retranchant 5 ça ne marchje pas a tous les coup
merci pour votre aide

[nix2016]

Salut

Tu es sûr que c'est x^3-x^2+6 +qu'il faut factoriser?

oui je suis sur Mr quand j aurai le manuel je te ferai une image

[Lostounet]

L'équation (machin=0)a bien une solution réelle (comme toute équation de degré 3 polynomiale donc continue qui passe de -l'infini à +l'infini et qui par le théorème des valeurs intermédiaires coupe quelque part l'axe des abscisses).

La difficulté est d'exprimer exactement la solution, ce qui est infaisable ici au niveau lycée. Il ya probablement une erreur d'énoncé (ce qui le laisse aussi penser: le + 3 + 3 parait redondant)

[nix2016]

[quote="Lostounet"]L'équation (machin=0)a bien une solution réelle (comme toute équation de degré 3 polynomiale donc continue qui passe de -l'infini à +l'infini et qui par le théorème des valeurs intermédiaires coupe quelque part l'axe des abscisses).

La difficulté est d'exprimer exactement la solution, ce qui est infaisable ici au niveau lycée. Il ya probablement une erreur d'énoncé (ce qui le laisse aussi penser: le + 3 + 3 parait redondc est juste pour des eleves de la premiere c est dans le cadre d une activité du chapitre identités remarquables

[Lostounet]

On peut avoir un énoncé complet, précis et exact s'il te plait?
Plutôt que de jouer aux devinettes :p

[chan79]

peut-être une erreur de frappe (ça arrive)
on peut factoriser

[zygomatique]

salut

je ne crois pas que ce soit cela : pourquoi "désordonner" tout d'un un polynome ....

par contre en regardant E(x) il semble plutôt raisonnable de penser à

[chan79]

en regardant E(x) il semble plutôt raisonnable de penser à

oui, ça doit être ça; pour une raison mystérieuse, le n'a pas été imprimé ...

[anthony_unac]

Bonsoir,
Les gars qui arrivent à déjouer les pièges(erreurs) des rédacteurs de manuel rhooo vous êtes bons, vous allez vraiment loin dans la réflexion

[zygomatique]

juste un peu d'expérience ... en regardant toujours l'énoncé complet ... pour se donner une idée ...

d'ailleurs on remarque que D(x) est aussi du même tonneau ...