Factorisation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Arkonk
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2013, 22:58
-
 par Arkonk » 05 Jan 2013, 15:42
par Arkonk » 05 Jan 2013, 15:42
Bonjour,
J'aurais besoin de votre aide s'il vous plaît, je n'arrive pas du tout à factoriser l'expression suivante :
^2-4)
Merci d'avance
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 05 Jan 2013, 16:01
par Carpate » 05 Jan 2013, 16:01
Arkonk a écrit:Bonjour,
J'aurais besoin de votre aide s'il vous plaît, je n'arrive pas du tout à factoriser l'expression suivante :
^2-4)
Merci d'avance
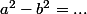
-
Arkonk
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2013, 22:58
-
 par Arkonk » 05 Jan 2013, 16:12
par Arkonk » 05 Jan 2013, 16:12
Carpate a écrit: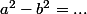
-4)
est de la forme
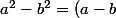(a+b))
avec
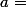

et
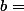

Justement je ne trouve pas

et

, j'ai suppose que
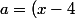)
et
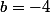
.
Je me trompe ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 05 Jan 2013, 16:20
par Carpate » 05 Jan 2013, 16:20
Arkonk a écrit:^2-4)
est de la forme
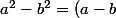(a+b))
avec
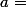

et
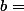

Justement je ne trouve pas

et

, j'ai suppose que
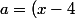)
et
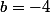
.
Je me trompe ?
On identifie (x-4)^2 -4 à a^2 - b^2
(x-4)^2 = a ^2, a = x - 4
4 = 2^2 = b^2
donc b = ...
-
Arkonk
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2013, 22:58
-
 par Arkonk » 06 Jan 2013, 15:20
par Arkonk » 06 Jan 2013, 15:20
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Jan 2013, 15:37
par Carpate » 06 Jan 2013, 15:37
-
Arkonk
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2013, 22:58
-
 par Arkonk » 06 Jan 2013, 15:39
par Arkonk » 06 Jan 2013, 15:39
Carpate a écrit:On identifie (x-4)^2 -4 à a^2 - b^2
(x-4)^2 = a ^2, a = x - 4
4 = 2^2 = b^2
donc b = ...
Salut !
J'ai trouvé cela :
^4 = [(x-4)-2][(x-4)+2])
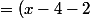(x-4+2))
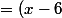(x-2))
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Jan 2013, 15:41
par Carpate » 06 Jan 2013, 15:41
Ton résultat est bon mais l'expression initiale était
^2-4)
et non
^4)
!
^2-4= (x-4)^2 -2^2= (x-4-2)(x-4+2)= (x-6)(x-2))
-
Arkonk
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2013, 22:58
-
 par Arkonk » 06 Jan 2013, 16:12
par Arkonk » 06 Jan 2013, 16:12
Carpate a écrit:Ton résultat est bon mais l'expression initiale était
^2-4)
et non
^4)
!
^2-4= (x-4)^2 -2^2= (x-4-2)(x-4+2)= (x-6)(x-2))
Effectivement je me suis bien trompé quand j'ai copier mais sur ma feuille j'ai bien écrit :
^2-4 = [(x-4)-2][(x-4)+2])
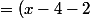(x-4+2))
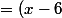(x-2))
Donc c'est bon ?
Est-ce que vous pouvez vérifier si cette équation est correcte s'il vous plaît ?
(x-2) = 0 \Leftrightarrow)

ou

Donc 6 et 2 sont les solutions de l'équation.
Merci d'avance.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Jan 2013, 17:04
par Carpate » 06 Jan 2013, 17:04
Arkonk a écrit:Effectivement je me suis bien trompé quand j'ai copier mais sur ma feuille j'ai bien écrit :
^2-4 = [(x-4)-2][(x-4)+2])
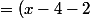(x-4+2))
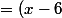(x-2))
Donc c'est bon ?
Est-ce que vous pouvez vérifier si cette équation est correcte s'il vous plaît ?
(x-2) = 0 \Leftrightarrow)

ou

Donc 6 et 2 sont les solutions de l'équation.
Merci d'avance.
C'est correct
-
Arkonk
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2013, 22:58
-
 par Arkonk » 06 Jan 2013, 17:12
par Arkonk » 06 Jan 2013, 17:12
Merci beaucoup de votre aide Carpate.
A bientôt peut être !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
et non
!