Factorisation d'un polynôme
15 messages
- Page 1 sur 1
Factorisation d'un polynôme
Bonjour,
Je souhaiterais savoir comment factoriser le polynôme suivant :
P(x) = 2x³ + 3x² - x – 2
Je connais la formule
(x-a)(x-b)(x-c)
Pour x³ + Px² + Qx + R avec P = - (a+b+c), Q= ab + bc + ca, R = - abc
Mais comme dans P(x) il y a le 2 devant x³, ben je sais pas comment m’y prendre…
Merci pour votre aide,
Ccil
Je souhaiterais savoir comment factoriser le polynôme suivant :
P(x) = 2x³ + 3x² - x – 2
Je connais la formule
(x-a)(x-b)(x-c)
Pour x³ + Px² + Qx + R avec P = - (a+b+c), Q= ab + bc + ca, R = - abc
Mais comme dans P(x) il y a le 2 devant x³, ben je sais pas comment m’y prendre…
Merci pour votre aide,
Ccil
Re: Factorisation d'un polynôme
Bonsoir,
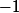 est racine évidente, car
est racine évidente, car ^3 + 3.(-1)^2 - (-1) - 2 = 0) , donc tu peux diviser P(x) par
, donc tu peux diviser P(x) par  ,
,
tu aura alors P(x) = (x + 1) (ax² + bx + c),
trouve alors les 2 racines de l'équation du second degré . . .
tu aura alors P(x) = (x + 1) (ax² + bx + c),
trouve alors les 2 racines de l'équation du second degré . . .
Re: Factorisation d'un polynôme
Merci Laetidom pour ta réponse, j'avais essayé avec -1 mais une fois que j'ai P(x) = (x + 1) (ax² + bx + c), je ne sais pas comment trouver mes a, b et c ni répartir les + et les - : j'ai essayé de deviner plusieurs solutions mais en redéveloppant pour vérifier je ne tombe pas juste, par exemple :
P(x) = (x + 1) (ax² + bx + c) = (x + 1) (2x² + 3x - 2) = 2x³ + 5x² + x – 2
après, trouver les deux racines de l'équation du second degré, je sais faire, mais avant il me faudrait la méthode pour déduire a, b et c, HELP !!! !
Ccil
P(x) = (x + 1) (ax² + bx + c) = (x + 1) (2x² + 3x - 2) = 2x³ + 5x² + x – 2
après, trouver les deux racines de l'équation du second degré, je sais faire, mais avant il me faudrait la méthode pour déduire a, b et c, HELP !!! !
Ccil
Re: Factorisation d'un polynôme
Bonsoir,
Il ne faut pas tâtonner pour trouver ,
,  et
et  , dans le sens où on se dit "je vais essayer
, dans le sens où on se dit "je vais essayer 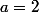 ,
, 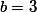 et
et 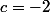 et j'espère que ça va marcher".
et j'espère que ça va marcher".
Développe plutôt(ax^2+bx+c)) et identifie les coefficients devant les puissances de x avec ceux que de
et identifie les coefficients devant les puissances de x avec ceux que de ) ...
...
Il ne faut pas tâtonner pour trouver
Développe plutôt
Re: Factorisation d'un polynôme
Bonsoir,
Il faut développer et réduire=(x+1)(ax^2+bx+c))
Tu trouves=ax^3+(a+b)x^2+(b+c)x+c)
Par identification tu obtiens le système suivant:

Ainsi,=(x+1)(2x^2+x-2)\right.)
NB: aussi, tu peux utiliser la méthode de la division euclidienne de polynômes.
Il faut développer et réduire
Tu trouves
Par identification tu obtiens le système suivant:
Ainsi,
NB: aussi, tu peux utiliser la méthode de la division euclidienne de polynômes.
Re: Factorisation d'un polynôme
Super merci samoufar et Al-Kashi, en parallèle je cherchais sur internet la méthode pour décomposer et du coup je comprends que c'est la même logique ! Je continue mes exercices, enfin... jusqu'aux prochains blocages !?!
Bonne soirée
Bonne soirée
Re: Factorisation d'un polynôme
Bonjour,
Ca marche aussi comme ça :

(division euclidienne)
Bonne journée @ tous !
Ca marche aussi comme ça :

(division euclidienne)
Bonne journée @ tous !
Re: Factorisation d'un polynôme
Bonjour à tous,
Et maintenant je souhaiterais trouver 4 inconnues a, b, c et d en décomposant la fonction suivante :
l(x) = 2x + 3
(x-1) ²(x² + 1)
Sous la forme l(x) = a + b + cx + d
(x-1) (x-1) ² (x² + 1)
En mettant tout sur le même dénominateur j’ai :
l(x) = a(x-1) (x² + 1) + b(x² + 1) + (cx + d) (x-1) ²
(x-1) ²(x² + 1)
A la finale j’arrive au système suivant : a + c = 0
b + c + d – a = 0
a + c – 2d = 2
-a + b + d = 3
Pour la suite, je ne vois pas comment m’y prendre…
Merci pour votre aide,
Ccil
Et maintenant je souhaiterais trouver 4 inconnues a, b, c et d en décomposant la fonction suivante :
l(x) = 2x + 3
(x-1) ²(x² + 1)
Sous la forme l(x) = a + b + cx + d
(x-1) (x-1) ² (x² + 1)
En mettant tout sur le même dénominateur j’ai :
l(x) = a(x-1) (x² + 1) + b(x² + 1) + (cx + d) (x-1) ²
(x-1) ²(x² + 1)
A la finale j’arrive au système suivant : a + c = 0
b + c + d – a = 0
a + c – 2d = 2
-a + b + d = 3
Pour la suite, je ne vois pas comment m’y prendre…
Merci pour votre aide,
Ccil
Re: Factorisation d'un polynôme
J'essaie de réécrire mieux pour que l'on comprenne : (c'est des fractions)
Bonjour à tous,
Et maintenant je souhaiterais trouver 4 inconnues a, b, c et d en décomposant la fonction suivante :
l(x) = 2x + 3
(x-1) ²(x² + 1)
Sous la forme l(x) = a + b + cx + d
(x-1) (x-1) ² (x² + 1)
En mettant tout sur le même dénominateur j’ai :
l(x) = a(x-1) (x² + 1) + b(x² + 1) + (cx + d) (x-1) ²
(x-1) ²(x² + 1)
A la finale j’arrive au système suivant :
a + c = 0
b + c + d – a = 0
a + c – 2d = 2
-a + b + d = 3
Pour la suite, je ne vois pas comment m’y prendre…
Merci pour votre aide,
Ccil
PS : il n'y a pas de traits mais c'est bien des fractions ! Je viens de me casser la tête à l'écrire lisiblement dans word et là la mise en page s'est supprimée....
Bonjour à tous,
Et maintenant je souhaiterais trouver 4 inconnues a, b, c et d en décomposant la fonction suivante :
l(x) = 2x + 3
(x-1) ²(x² + 1)
Sous la forme l(x) = a + b + cx + d
(x-1) (x-1) ² (x² + 1)
En mettant tout sur le même dénominateur j’ai :
l(x) = a(x-1) (x² + 1) + b(x² + 1) + (cx + d) (x-1) ²
(x-1) ²(x² + 1)
A la finale j’arrive au système suivant :
a + c = 0
b + c + d – a = 0
a + c – 2d = 2
-a + b + d = 3
Pour la suite, je ne vois pas comment m’y prendre…
Merci pour votre aide,
Ccil
PS : il n'y a pas de traits mais c'est bien des fractions ! Je viens de me casser la tête à l'écrire lisiblement dans word et là la mise en page s'est supprimée....
Re: Factorisation d'un polynôme
Bonsoir,
D'abord désolé que tu aies dû te casser la tête à tout mettre en page sur Word, mais bon il faillait un peu s'y attendre Résultat des courses, c'est difficile à lire... Sinon, avec le scan c'est tout de suite bien mieux
Résultat des courses, c'est difficile à lire... Sinon, avec le scan c'est tout de suite bien mieux 
Cette opération s'appelle une décomposition en éléments simples. Tu peux y aller comme tu as fait en réduisant au même dénominateur et en résolvant le système à 4 équations (ici il se résout plutôt bien, par exemple les lignes 1 et 3 te donnent d=-1, etc.). Mais généralement c'est suicidaire
Mais bon on va quand même faire comme ça.
- La ligne 1 te dit que a = -c. Donc si tu trouves c, tu as immédiatement a. Donc tu peux remplacer a par -c dans les lignes 2, 3 et 4.
- Tu as donc
a = -c
b - c + d = 0
-2d = 2
b + c + d = 3
- Les lignes 2, 3 et 4 forment un système à 3 équations. En faisant comme ce qui précède, tu te ramènes à deux équations, puis une seule, et c'est bon
D'abord désolé que tu aies dû te casser la tête à tout mettre en page sur Word, mais bon il faillait un peu s'y attendre
Pour une jolie (et surtout lisible) mise en page, tu peux utiliser les formules LaTeX (bouton "tex" en haut à droite ou "éditeur d'équation" qui est plutôt bien fait). Voilà notamment un exemple :
\dfrac{a}{b} ->
3x^3-2x^2+x+1 ->
Cette opération s'appelle une décomposition en éléments simples. Tu peux y aller comme tu as fait en réduisant au même dénominateur et en résolvant le système à 4 équations (ici il se résout plutôt bien, par exemple les lignes 1 et 3 te donnent d=-1, etc.). Mais généralement c'est suicidaire
Mais bon on va quand même faire comme ça.
- La ligne 1 te dit que a = -c. Donc si tu trouves c, tu as immédiatement a. Donc tu peux remplacer a par -c dans les lignes 2, 3 et 4.
- Tu as donc
a = -c
b - c + d = 0
-2d = 2
b + c + d = 3
- Les lignes 2, 3 et 4 forment un système à 3 équations. En faisant comme ce qui précède, tu te ramènes à deux équations, puis une seule, et c'est bon
Modifié en dernier par samoufar le 11 Fév 2017, 19:24, modifié 1 fois.
Re: Factorisation d'un polynôme
Bonsoir Ccil,
Tu as une erreur à la dernière ligne. Le coefficient de serait
serait  .
.
Le système à résoudre est :

En résolvant le système, tu dois trouver:
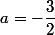


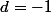
Tu as une erreur à la dernière ligne. Le coefficient de
Le système à résoudre est :
En résolvant le système, tu dois trouver:
Re: Factorisation d'un polynôme
Merci samoufar et Al-Kashi, je viens de refaire toutes les étapes et c'est tout bon, du coup, j'ai du mal à comprendre pourquoi j'ai buté dessus... La fatigue sûrement 
A+
Ccil
A+
Ccil
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
