bonjours voila je oudrais de l'ide concernant la factorisation d'un polinome du second degré pour obtenir
la forma (x+a)(x+b)
il y a t-il d'autres solutions que delta ?
par exemple :
25x²-15x+4 ?
cordialement jonathan Leroy
Facorisation de trinome
6 messages
- Page 1 sur 1
Salut, il y a des tas de façons d'obtenir une factorisation qui tournent toutes autours de la forme canonique, mais par exemple dans le cas de 25x²-15x+4, tu ne risque pas de l'écrire (x-a)(x-b) vu que le coeff. en x² n'est pas le même dans les deux cas.
Sinon, on peut par exemple écrire que :
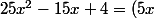^2-2\times 5x \times \frac{3}{2}+(\frac{3}{2})^2+4-(\frac{3}{2})^2) , c'est à dire que tu fait, comme d'habitude, apparaitre une identité remarquable.
, c'est à dire que tu fait, comme d'habitude, apparaitre une identité remarquable.
Donc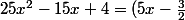^2+\frac{7}{4}) et tu ne peut pas factoriser plus vu que la quantité en question ne s'annule jamais (elle est toujours
et tu ne peut pas factoriser plus vu que la quantité en question ne s'annule jamais (elle est toujours  )
)
Sinon, on peut par exemple écrire que :
Donc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
réponse
Ben314 a écrit:Salut, il y a des tas de façons d'obtenir une factorisation qui tournent toutes autours de la forme canonique, mais par exemple dans le cas de 25x²-15x+4, tu ne risque pas de l'écrire (x-a)(x-b) vu que le coeff. en x² n'est pas le même dans les deux cas.
Sinon, on peut par exemple écrire que :, c'est à dire que tu fait, comme d'habitude, apparaitre une identité remarquable.
Doncet tu ne peut pas factoriser plus vu que la quantité en question ne s'annule jamais (elle est toujours
)
merci neanmoins je n'ai pas tout compris sur ton developpement ( ps j'ai quitté la série scientifique il y a déja 6 ans j'ai pas mal oublié les cours :/)
merci
bjr
25x²-15x+4 ?
M.Ben te montre la forme a²-2ab+b² -b² +4 pour arriver à la forme (a-b)² -b²+4
on pose :
a²=25x²
2ab=-15x
avec b=-15x/2a=-15x/10x=-3/2
pour obtenir
(5x-3/2)² -(3/2)² +4
(5x-3/2) ² -9/4 +16/4
(5x -3/2)² +7/4 pour le moment tu ne peux plus factoriser dans les réels
plus tard avec les complexes tu obtiendras la factorisation
en posant le complexe i²=-1
(5x -3/2)² +7/4=(5x -3/2)² -i²(7/4)
racine carré (7/4)=V(7/4)
de la forme A²-B²= (A-B)(A+B)= [5x-3/2 -iV(7/4)][5x-3/2 +iV(7/4)]
25x²-15x+4 ?
M.Ben te montre la forme a²-2ab+b² -b² +4 pour arriver à la forme (a-b)² -b²+4
on pose :
a²=25x²
2ab=-15x
avec b=-15x/2a=-15x/10x=-3/2
pour obtenir
(5x-3/2)² -(3/2)² +4
(5x-3/2) ² -9/4 +16/4
(5x -3/2)² +7/4 pour le moment tu ne peux plus factoriser dans les réels
plus tard avec les complexes tu obtiendras la factorisation
en posant le complexe i²=-1
(5x -3/2)² +7/4=(5x -3/2)² -i²(7/4)
racine carré (7/4)=V(7/4)
de la forme A²-B²= (A-B)(A+B)= [5x-3/2 -iV(7/4)][5x-3/2 +iV(7/4)]
Il faut tout de même donner un bref coup d'oeil au delta, et 25x²-15x+4=0 , n'a pas de racines donc impossible à factoriser, il faut passer par les imaginaires.
autrement pour éviter le delta, il faut essayer de voir s'il y a une racine apparente
exemple x²+3x-4=0, on voit que d'après les coefficients f(1)=0 donc x'=1
On sait que c/a= x'x"" donc -4=1.x" d'ou x"=-4
donc on peut écrire (x-1)(x+4)...
En général on essaye 1 ou -1 jusqu'à 5 ou -5... après..
autrement pour éviter le delta, il faut essayer de voir s'il y a une racine apparente
exemple x²+3x-4=0, on voit que d'après les coefficients f(1)=0 donc x'=1
On sait que c/a= x'x"" donc -4=1.x" d'ou x"=-4
donc on peut écrire (x-1)(x+4)...
En général on essaye 1 ou -1 jusqu'à 5 ou -5... après..
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
