Expressions constante à démontrer de manière directe ou après calcul de la dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
dadaclecle
- Membre Naturel
- Messages: 66
- Enregistré le: 21 Jan 2015, 14:33
-
 par dadaclecle » 01 Déc 2015, 20:14
par dadaclecle » 01 Déc 2015, 20:14
Bonsoir,
On me demande de vérifier que les expressions suivantes sont constantes, par un calcul direct, puis par le calcul de la dérivée:
( sinx) puissance 6 + (cosx)puissance 6 + (sinx)puissance4 (cosx)puissance4 + 5sin²x.cos²x
et deuxième expression
(sinx)puissance 8 + (cosx)puissance8 + 4sin²x.cos²x - 2(sinx)puissance4.(cosx) puissance4
Par le calcul direct, je ne sais pas par où commencer . Faut-il supposer que quelque soit x1 et x2 on a une égalité ... faut-il commencer par des transformations ?
Je sais calculer la dérivée de ces expressions ( trop long à écrire ici avec le peu de moyen d'écriture dont je dispose...) et après je rencontre le même problème pour montrer que ces dévirées sont nulles!
Merci pour votre aide
Cordialement

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Déc 2015, 20:23
par zygomatique » 01 Déc 2015, 20:23
salut
un exemple de transformation ....
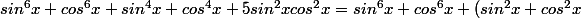^2 + 3sin^2xcos^2x = ...)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Déc 2015, 20:23
par siger » 01 Déc 2015, 20:23
bonsoir
commence par tout ecrire en fonction d'une seule fonction trigonométrique
sinx^6 + (1-sinx^2)^3 + sinx^4 + (1-sinx^2)^2 + 5sinx^2(1-sinx^2)
par exemple
.....

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Déc 2015, 20:40
par zygomatique » 01 Déc 2015, 20:40
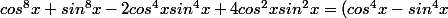^2 + 4cos^2xsin^2x = (cos^2x - sin^2x)^2 + 4cos^2xsin^2x = cos^4x + 2cos^2xsin^2x + sin^4x = (cos^2x + sin^2x)^2 = 1)
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
dadaclecle
- Membre Naturel
- Messages: 66
- Enregistré le: 21 Jan 2015, 14:33
-
 par dadaclecle » 01 Déc 2015, 21:00
par dadaclecle » 01 Déc 2015, 21:00
zygomatique a écrit:salut
un exemple de transformation ....
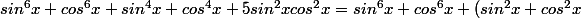^2 + 3sin^2xcos^2x = ...)
donc sin^6x + cos^6x + 1 + 3sin^2cos^2 et je suis encore bloqué !
-
dadaclecle
- Membre Naturel
- Messages: 66
- Enregistré le: 21 Jan 2015, 14:33
-
 par dadaclecle » 01 Déc 2015, 21:02
par dadaclecle » 01 Déc 2015, 21:02
siger a écrit:bonsoir
commence par tout ecrire en fonction d'une seule fonction trigonométrique
sinx^6 + (1-sinx^2)^3 + sinx^4 + (1-sinx^2)^2 + 5sinx^2(1-sinx^2)
par exemple
.....
Merci donc je trouve:
3sin^4 - 5 sin^3x - 5sin^2x + 5sinx +2 et après je ne sais pas quoi en faire de cette expression !
-
dadaclecle
- Membre Naturel
- Messages: 66
- Enregistré le: 21 Jan 2015, 14:33
-
 par dadaclecle » 01 Déc 2015, 21:09
par dadaclecle » 01 Déc 2015, 21:09
zygomatique a écrit: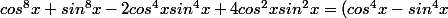^2 + 4cos^2xsin^2x = (cos^2x - sin^2x)^2 + 4cos^2xsin^2x = cos^4x + 2cos^2xsin^2x + sin^4x = (cos^2x + sin^2x)^2 = 1)
:ptdr:
oui il fallait donc voir la différence de deux carrés dans lexpression (cos^4x - sin^4x)² avec cos²x + sin²x =1.
Merci beaucoup

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 01 Déc 2015, 21:10
par chan79 » 01 Déc 2015, 21:10
une variante
Développe:
(cos²x+sin²x)³=
(cos²x+sin²x)²=
En ajoutant, tu as vite la réponse
PS il manque un signe + dans ta première expression
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 01 Déc 2015, 21:14
par Pisigma » 01 Déc 2015, 21:14
dadaclecle a écrit:donc sin^6x + cos^6x + 1 + 3sin^2cos^2 et je suis encore bloqué !
Bonsoir,
+cos^2(x))^3-3sin^4(x)cos^2(x)-3sin^2(x)cos^4(x)+1+3sin^2(x)cos^2(x)=...)
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 02 Déc 2015, 14:35
par siger » 02 Déc 2015, 14:35
Re
dadaclecle a écrit:Merci donc je trouve:
3sin^4 - 5 sin^3x - 5sin^2x + 5sinx +2 et après je ne sais pas quoi en faire de cette expression !
sinx^6 + (1-sinx^2)^3 + sinx^4 + (1-sinx^2)^2 + 5sinx^2(1-sinx^2)
= sinx^6+ (1-3sinx^2+3sinx^4 - sinx^6) + sinx^4 + (1- 2sinx^2 +sinx^4) +5sinx^2-5sinx^4) = 2
-
dadaclecle
- Membre Naturel
- Messages: 66
- Enregistré le: 21 Jan 2015, 14:33
-
 par dadaclecle » 02 Déc 2015, 21:04
par dadaclecle » 02 Déc 2015, 21:04
siger a écrit:Re
sinx^6 + (1-sinx^2)^3 + sinx^4 + (1-sinx^2)^2 + 5sinx^2(1-sinx^2)
= sinx^6+ (1-3sinx^2+3sinx^4 - sinx^6) + sinx^4 + (1- 2sinx^2 +sinx^4) +5sinx^2-5sinx^4) = 2
Il suffisait donc de développer ... Merci beaucoup.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
