Expression positive

[Benjamin]

Bonjour,

Je crois que Titux est en seconde, donc a priori, il ne sait pas ce qu'est la dérivée ^^

[Nightmare]

Je suis sûr que si :lol3:

[Olympus]

Tiens, encore un de tes Khôlles que je mets dans mes marque-pages ( si t'as rédigé un .pdf avec tous tes Khôlles, je suis preneur :D ) pour plus tard quand j'aurais des notions solides en intégration, continuité etc... ^^

[Anonyme]

Je suis sür que si

C'est ironique ?

Merci Olympus. Je dois ensuite obtenir sans calto les dix premières décimales du développement décimal de V(64,00032). Comment chosir a et h ?

[Olympus]

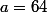
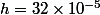
Pose et et applique la dernière inégalité .

[Anonyme]

J'avais pensé à ça un peu...

J'obtiens :

0<8+4.10^-5-V(64,00032)<10^-10/4

[Olympus]

Ok, encadre avec ça .

EDIT : t'as fait des fautes de calcul je crois, ressaie .

[Anonyme]

Je vois pas trop ou !

[Anonyme]

Quelqu'un voit où je me suis planté, s'il vous plaît ? ;p

[Olympus]

Ben c'est plutôt .

Soit :

.

Ensuite, tu conclu .

( PS : c'est en aucun cas une attaque, mais faut pas bloquer sur ce genre d'exos si tu comptes rentrer en 1ère S ... Multiplier par le conjugué ( cf. la question précédente ) par exemple doit être un des réflexes que tu dois avoir pendant toute l'année . )

[Anonyme]

Ah c'est sur qu'un 4 à la place d'un 2 c'est "des erreurs de calcul"...
Je penserai au conjugué, même si je n'aurais pas ce genre d'exos hors-prog...
En France, on a le mérite de rester un minimum réaliste.

[Olympus]

Calcul de limites, le signe de la dérivée etc... non, tu auras toujours besoin de ce réflexe ;-)

[Anonyme]

Non mais je sais calculer les limites en utilisant cela, mais ici je n'y ai pas pensé, c'est tout.