Expression littérale...

[mjdd]

Bonjour a tous je bute un peu sur cet exercice simplifier:

cordialement...

[capitaine nuggets]

Salut !

Je pense qu'on ne pourra pas y échapper : il faut trouver un dénominateur commun.
En regardant plus attentivement les dénominateurs, quel sera le meilleur dénominateur commun ?

[mjdd]

salut en effet oui et ici c'est (a-b)(a-c)(b-c) mais pour simplifier après c'est la ou je bute.

[capitaine nuggets]

Admettons, donne-nous ce que tu obtiens au numérateur seulement

[mjdd]

Salut...

[anthony_unac]

Bonsoir,
Cela semble correct mais je ne vois pas de simplification miraculeuse dans cette affaire. J'ai cru un peu vite qu'on pouvait encore simplifier en utilisant l'identité de la somme de 3 cubes et notamment cette égalité : ou le second membre ressemble curieusement à votre dénominateur commun mais bof ...

[mjdd]

Salut je vais essayer cette piste j'avoue que j'ai essayé toutes mes petite magies qui m'ont souvent sauvé la vie mais jusque la rien.
cordialement...

[Pseuda]

Bonjour,

Prends quelques valeurs pour (a,b,c), par exemple : a=2, b=1, c=0 ou a=2, b=1, c=-1, on trouve à chaque fois a+b+c pour l'expression.

Il ne reste plus qu'à le démontrer.

[Ben314]

Salut,
La question que tu te pose, en fait, c'est de savoir si on peut simplifier le numérateur avec le dénominateur donc, par exemple, si on peut factoriser (a-b) dans le numérateur.
Et si on veut utiliser un peu de théorie et ne pas tout faire "à la main", la façon de voir le truc, c'est de dire que b et c sont supposés connus (c'est des constantes) et que a est une variable.
Pour que ça colle mieux avec l'écriture usuelle variable/constante, ça veut juste dire qu'on prend a=X sans toucher au reste.
Le numérateur est alors et, pour voir si ce polynôme est ou pas divisible par (=a-b), il suffit de regarder s'il s'annule lorsque .
Et une fois que tu as vérifié que c'est bien le cas, tu peut par exemple procéder par identification pour trouver le polynôme Q(X) tel que .
Tu peut même aller un peu plus vite en constatant que le polynôme s'annule aussi pour et chercher directement (par identification) le polynôme R(X) tel que .

[Pseuda]

Bonjour,

Merci Ben314. C'est une méthode à retenir. Dès lors (cela me fait penser), on peut proposer à notre lycéen une méthode intermédiaire, en cherchant une factorisation par de .

,
etc..., réduction du crochet,
puis factorisation du crochet par , puis par .

Encore faut-il savoir factoriser .

[Ben314]

Tu peut aussi le faire comme le ferais sans doute un élève de Lycée, c'est à dire "par identification" (je remet des X à la place de a pour que ça soit plus clair) :
Vu qu'il s'annule pour X=b et X=c, on sait qu'on peut factoriser (X-b) et (X-c) dans le polynôme et, comme il est de degré 3, le troisième facteur est de degré 1 donc en fait
où et sont deux constantes.
En développant les termes de droite et de gauche de l'égalité, puis en identifiant les coefficients, on obtient 4 équations concernant les deux inconnues et mais comme on n'a que deux inconnues et qu'on sait d'avance qu'il existe une solution à ce système , on peut se contenter de deux équations (cette partie là, je suis bien d'accord que c'est sans doute pas un truc qui viendrait à l'esprit d'un Lycéen actuel : faire du raisonnement pour éviter des calculs, c'est pas trop la mode ces derniers temps...).
En regardant l'équation venant de l'égalité des coeff. en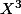 on obtient .
Et en regardant celle venant de l'égalité des coeff. en on obtient donc
(et le Lycéen "standard" vérifierais sans doute que les deux dernières équations sont elle aussi vérifiées, bien que ce ne soit pas utile)
Conclusion :

[anthony_unac]

Bonjour,
... et au final on factorise le numérateur et le dénominateur par (X-b) qui est égal à (a-b), puis on simplifie (sous réserve que a est différent de b) mais après ... ?
Il reste toujours une expression qui est loin d'être simplifiée par rapport à l'expression de départ ou alors j'ai loupé un truc ?!

[anthony_unac]

Donc j'ai loupé un truc car le résultat final serait -(a+b+c) ?

[Ben314]

... et au final on factorise le numérateur et le dénominateur par (X-b) qui est égal à (a-b), puis on simplifie (sous réserve que a est différent de b) mais après ... ?
Il reste toujours une expression qui est loin d'être simplifiée par rapport à l'expression de départ ou alors j'ai loupé un truc ?!

Je pense qu'effectivement tu as "loupé (au moins) un truc" :
- Le dénominateur, comme toujours dans un cas tel que celui là, on l'a directement sous forme factorisé, à savoir (a-b)(a-c)(b-c)
- Et le numérateur, la factorisation qu'on obtient (c.f. post. çi dessus), c'est (b-c)(a-b)(a-c)(a+b+c)
- Ensuite, le fait que a,b,c doivent être distinct, c'est pas franchement "une réserve sous laquelle on peut simplifier", mais plutôt une obligation absolue pour que l'énoncé initial ait un sens (i.e. ne contienne pas de division par 0)
- Et enfin, une fois qu'on a simplifié numérateur et dénominateur, on obtient a+b+c et, personnellement moi-même, il me semble bien que je n'emploierais pas le terme de "loin d'être simplifiée" pour désigner une telle expression.

[Pseuda]

@Ben314

La factorisation générale des polynômes n'est pas au programme du lycée, donc pour la solution avec les polynômes, il faut les aider un peu.
En factorisant directement (et en les aidant aussi un peu), on peut se passer de résoudre une équation. Mais c'est mon opinion personnelle.

[Ben314]

Je ne sais pas ce qui est au programme du Lycée, mais déjà, je ne pense pas avoir dit (ni même sous entendu) que la méthode que je proposait était "mieux" que les autres et ensuite, tant qu'à faire du "un peu hors programme", j'aurais tendance à très nettement préféré un "vrai résultat" du style "Si P(a)=0 alors on peut factoriser (X-a) dans P(X)" plutôt qu'une "identité remarquable" supplémentaire style .
A mon avis, en particulier du fait des stats., il y a plus qu'assez de "formules à apprendre par cœur" dans les programmes actuels pour que ce soit pas vraiment utile d'en rajouter d'autres : je me demande quand même assez souvent si l'incompétence flagrante d'un grand nombre de Lycéens à construire un quelconque raisonnement, ça viendrait pas, au moins en partie, de la façon dont on présente de plus en plus les maths, à savoir comme des recettes à appliquer (mais il faut bien avouer que c'est un peu le problème de l'œuf et de la poule...)

Et j'insiste de nouveau en disant bien que c'est uniquement mon opinion (que je partage avec moi même) donc que ça vaut... ce que ça vaut...

P.S. Par contre, je comprend pas bien ton "on peut se passer de résoudre une équation" : avec quelle méthode et à quel endroit considère tu qu'on "résous une équation" ?

[Ben314]

Et sinon, une autre méthode qui me semblerais parfaitement accessible au Lycée (et qui a le bon gout d'être très générale, y compris pour montrer des résultats théoriques), c'est de faire un/des changement de variables : autant face à un polynôme (en une ou plusieurs variable), c'est pas complètement évident de voir s'il est divisible par exemple par X-a, autant pour voir s'il est ou pas divisible par X, c'est évident : il suffit de développer tel le bourrin et de regarder s'il y a ou pas un terme constant.
Ici, ça consisterait par exemple à poser (donc ) et (donc ) puis, partant de à réduire au même dénominateur et à développer sans réfléchir le numérateur : il apparaitrait alors très clairement que ce dernier est divisible par 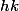(puis, après simplification, à peine moins clairement que ce qui reste est divisible par )

[Pseuda]

C'est aussi mon opinion. Dans les 2 cas, il faut aider. Le théorème fondamental de l'algèbre qui induit : "si P(a)=0, alors le polynôme se factorise par (X-a)" n'est pas au programme du lycée.

Equations ??? mais c'est toi qui en parle. Que sont les inconnues u et v alors ?

La dernière méthode est intéressante aussi, mais elle ne viendrait pas tout de suite à l'esprit, et d'un lycéen, il faudrait aider alors.

[Ben314]

Effectivement tu as tout à fait raison concernant les équations (je crois que j'ai un peu tendance à faire comme si, tout ce qui est linéaire, c'est "pas vraiment" des équations alors qu'il n'y a pas de doute...)

[chan79]

salut
une autre approche
on peut remarquer que si on multiplie chaque lettre par k, l'expression est multipliée par k.
On pose A=a/c et B=b/c C=1
On remplace donc a, b et c par A, B et 1 dans l'expression, et à la fin on multiplie le résultat par c.
Ensuite, un peu de calcul ... mais avec deux lettres






A+B+1
Le résultat est Ac+Bc+c=a+b+c