Exponentielle

[Snipy]

Bonjour, j'ai une petite question

J'ai la fonction dérivée g'(x)= exp(x-4) + (x+2)exp(x-4) = 0

Apres m'avoir trompé au bac blanc je me suis rendue compte qu'il fallait factorise de la façon de (x+3)exp(x-4) et résoudre (x+3)

mais voila je comprends pas trop pour quoi on factorise on ne peut pas résoudre : exp(x-4) + x exp(x-4) + 2exp(x-4) et si oui comment car j'arrive pas

Merci d'avance

[Carpate]

je comprends pas trop pour quoi on factorise

Parce qu'on aboutit ainsi à une équation produit * et ça on sait faire ...
Sinon comment pourrait-on résoudre cette équation ?

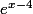
(*) équation produit dont l'un des 2 termes : n'est jamais nul

[Sylviel]

Bonjour,

ton message n'est vraiment pas clair. J'imagine que tu cherches à résoudre
exp(x-4) + (x+2)exp(x-4) = 0 ?

Dans ce cas tu peux factoriser par exp(x-4) pour avoir
exp(x-4) + (x+2)exp(x-4) = [1 + (x+2)]exp(x-4) = 0
Ensuite, comme exp(x-4) n'est jamais nul, tu peux diviser de chauqe côté par exp(x-4) pour avoir
x+3 = 0, d'où x=-3

Si tu développes exp(x-4) + (x+2)exp(x-4) pour écrire exp(x-4) + x exp(x-4) + 2exp(x-4) =0, cela ne t'avance pas beaucoup, mais tu peux toujours diviser par exp(x-4) de chaque côté pour obtenie
1 + x + 2 =0.

[Snipy]

oui en effet je cherche : exp(x-4) + (x+2)exp(x-4) = 0 ?

mais surtout je cherchais a comprendre mon erreur : qui est que a la place de diviser exp(x-4) + x exp(x-4) + 2exp(x-4) par exp(x-4) , j'ai fais :

exp(x-4) + x exp(x-4) + 2exp(x-4) = 0
exp(x-4) + exp (x-4) +2 exp(x-4) = 0/x donc si j'ai bien compris cette ligne est fausse mais je comprends pas pourquoi ces faux
exp(x-4) + exp (x-4) + exp(x-4) = 0/2 = 0
x-4 + x-4 + x-4 =0
3x-12=0
3x=12
x=4

[Carpate]

On factorise :


Solution unique

[Snipy]

oui mais pourquoi on est obligé de factorise ?, c'est que j'arrive pas a comprendre

[Carpate]

oui mais pourquoi on est obligé de factoriser ?, c'est que j'arrive pas a comprendre

Parce qu'on ne sait résoudre pratiquement que des équations produits.

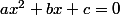
Par exemple, pour résoudre l'équation du second degré , on la met sous sa forme canonique :

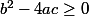
On ne fait pas ça pour s'amuser mais parce que si , l'équation se met sous la forme de diférence de 2 carrées :

qui se factorise en une équation produit :

Et là c'est fini !

[vam]

bonjour

exp(x-4) + x exp(x-4) + 2exp(x-4) = 0
exp(x-4) + exp (x-4) +2 exp(x-4) = 0/x donc si j'ai bien compris cette ligne est fausse mais je comprends pas pourquoi ces faux

parce que s'il te prend l'envie de diviser à droite par x tu dois diviser tout le membre de gauche également par x et pas seulement 1 seul terme

ensuite diviser par l'inconnue, c'est très risqué...car si 0 est solution ....

[Snipy]

Ahhh oui merci je suis vraiment bête avec le stress j ai oublié...

[Carpate]

Et en plus, même avec la précaution d'écarter le cas x = 0, cette factorisation par x est vraiment gratuite et ne t'avance à rien ...