Bonsoir,
j'ai un petit problème que je n'arrive pas à résoudre
f(x)=xexp(x) si x < OU égal à 1
f(x)= ax+b si x > 1
a) valeurs de a et b pour que f soit continue en 1
b) valeurs de a et b pour que f soit dérivable en 1
Pour la question a je trouve a+b=e mais cela ne m'indique rien ni sur a ni sur b
Et pour la b, je ne trouve pas du tout.
Si vous pouviez m'aider, ce serait gentil.
Merci
Exponentielle, continuité et dérivabilité
8 messages
- Page 1 sur 1
pour qu'elle soit continue il faut que les deux expression donne la même valeur en 1. Donc effectivement tu as trouvé a+b=e
Pour qu'elle soit dérivable, c'est pareil, il faut que la valeur de la dérivée en 1 soit la même pour les deux expressions.
la dérivée de ax+b c'est a
la dérivée de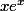 en 1 ça vaut quoi ?
en 1 ça vaut quoi ?
Pour qu'elle soit dérivable, c'est pareil, il faut que la valeur de la dérivée en 1 soit la même pour les deux expressions.
la dérivée de ax+b c'est a
la dérivée de
Et bien la dérivée de x.exp(x) c'est x.exp(x) et donc la dérivée en 1 c'est e.
Est-ce que cela veut dire que a=e ? Mais b égale quoi ? b=0 ?
Parce qu'à la calculette , ça me donne à l'intersection des 2 courbes une sorte d'angle, et j'avais appris que s'il y avait un angle, ce n'était pas dérivable ?
Est-ce que cela veut dire que a=e ? Mais b égale quoi ? b=0 ?
Parce qu'à la calculette , ça me donne à l'intersection des 2 courbes une sorte d'angle, et j'avais appris que s'il y avait un angle, ce n'était pas dérivable ?
Impiger a écrit:Et bien la dérivée de x.exp(x) c'est x.exp(x) et donc la dérivée en 1 c'est e.
Est-ce que cela veut dire que a=e ? Mais b égale quoi ? b=0 ?
Parce qu'à la calculette , ça me donne à l'intersection des 2 courbes une sorte d'angle, et j'avais appris que s'il y avait un angle, ce n'était pas dérivable ?
Pour x u'(x) = ...
v(x) = e^x ---> v'(x) = ...
f '(x) = ...
f '(1) = ...
*********
Pour x > 1
f(x) = (ax + b)
f '(x) = ...
lim(x-> +1+) f '(x) = ...
:zen:
Impiger a écrit:Ah oui j'avais oublié, merci
donc
Pour x1 f(x)=ax+b
f '(x) = a
Donc a=2e ?
Mais b alors ? Je ne vois pas comment on fait pour y revenir ?
Dans ton premier message, tu as écris: je trouve a+b=e
Dans ton dernier message, tu as écrit : a=2e
Avec ces 2 relations, il est facile de trouver les valeurs de a et de b ...
:zen:
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
