Expliciter la suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 16 Mai 2013, 21:02
par upium666 » 16 Mai 2013, 21:02
Bonjour à tous et à toutes !
Je poste ce message ici car vous avez plus d'"expérience" que les lycéens (eh oui, en suites, par exemple pour déterminer une suite auxiliaire, il faut en avoir vues !)

Exprimer

en fonction de

Merci

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 16 Mai 2013, 21:09
par Lostounet » 16 Mai 2013, 21:09
upium666 a écrit:Bonjour à tous et à toutes !
Je poste ce message ici car vous avez plus d'"expérience" que les lycéens (eh oui, en suites, par exemple pour déterminer une suite auxiliaire, il faut en avoir vues !)

Exprimer

en fonction de

Merci
Umm...
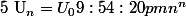
..?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 16 Mai 2013, 21:44
par upium666 » 16 Mai 2013, 21:44
Lostounet a écrit:Umm...
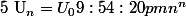
..?
Malheureusement ça ne marche pas :/
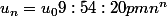
=>
^{n+1} \neq u_0 \cdot n^{n+1})

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 16 Mai 2013, 22:06
par Lostounet » 16 Mai 2013, 22:06
upium666 a écrit:Malheureusement ça ne marche pas :/
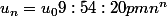
=>
^{n+1} \neq u_0 \cdot n^{n+1})
Hein?
Tu as défini une suite géométrique !
Chaque terme s'obtient en multipliant le précédent par une constante. Revois ton cours :p
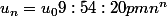
=>
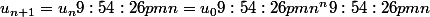
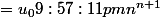
Tu n'augmentes pas la raison de la suite géométrique ! Je te conseille de la noter q, car tu sembles confondre le 'rang' du terme et la raison q !
Considère donc:
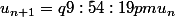
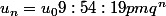
Et donc:
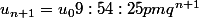
See, le q ne devient pas (q + 1) :p
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 16 Mai 2013, 22:20
par mrif » 16 Mai 2013, 22:20
Lostounet a écrit:Hein?
Tu as défini une suite géométrique !
Chaque terme s'obtient en multipliant le précédent par une constante. Revois ton cours :p
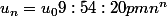
=>
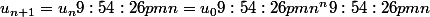
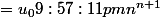
Tu n'augmentes pas la raison de la suite géométrique ! Je te conseille de la noter q, car tu sembles confondre le 'rang' du terme et la raison q !
Considère donc:
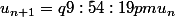
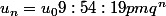
Et donc:
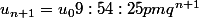
See, le q ne devient pas (q + 1) :p
n n'est pas une constante:
u25 = 24u24
u6 = 5u5
La réponse est
!u_1)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 16 Mai 2013, 22:24
par Lostounet » 16 Mai 2013, 22:24
mrif a écrit:n n'est pas une constante:
u25 = 24u24
u6 = 5u5
La réponse est
!u_1)
Ah je m'en doutais !
Je n'ai rien dit, alors ! Désolé :p
Oui bien entendu.
Je ne pense pas qu'il soit nécessaire d'introduire une suite auxiliaire car à chaque fois on multiplie par le n suivant, non? Une petite récurrence devrait suffire.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 16 Mai 2013, 22:43
par mrif » 16 Mai 2013, 22:43
Lostounet a écrit:Ah je m'en doutais !
Je n'ai rien dit, alors ! Désolé :p
Oui bien entendu.
Je ne pense pas qu'il soit nécessaire d'introduire une suite auxiliaire car à chaque fois on multiplie par le n suivant, non? Une petite récurrence devrait suffire.
Oui une petite récurrence suffit pour établir que
!u_1)
-
spike0789
- Membre Relatif
- Messages: 131
- Enregistré le: 06 Mai 2013, 10:50
-
 par spike0789 » 17 Mai 2013, 09:07
par spike0789 » 17 Mai 2013, 09:07
Salut,
Ou bien un produit télescopique avec U(n+1)/U(n)=n :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
en fonction de
=>
=>